Cantellated 24-cells
 24-cell |
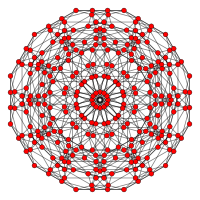 Cantellated 24-cell |
 Cantitruncated 24-cell |
| Orthogonal projections in F4 Coxeter plane | ||
|---|---|---|
In four-dimensional geometry, a cantellated 24-cell is a convex uniform 4-polytope, being a cantellation (a 2nd order truncation) of the regular 24-cell.
There are 2 unique degrees of cantellations of the 24-cell including permutations with truncations.
Cantellated 24-cell
| Cantellated 24-cell | ||
|---|---|---|
| Type | Uniform 4-polytope | |
| Schläfli symbol | rr{3,4,3} s2{3,4,3} | |
| Coxeter diagram | ||
| Cells | 144 | 24 24 96 |
| Faces | 720 | 288 triangles 432 squares |
| Edges | 864 | |
| Vertices | 288 | |
| Vertex figure |  Irreg. triangular prism | |
| Symmetry group | F4, [3,4,3] | |
| Properties | convex | |
| Uniform index | 24 25 26 | |
The cantellated 24-cell or small rhombated icositetrachoron is a uniform 4-polytope.
The boundary of the cantellated 24-cell is composed of 24 truncated octahedral cells, 24 cuboctahedral cells and 96 triangular prisms. Together they have 288 triangular faces, 432 square faces, 864 edges, and 288 vertices.
Construction
When the cantellation process is applied to 24-cell, each of the 24 octahedra becomes a small rhombicuboctahedron. In addition however, since each octahedra's edge was previously shared with two other octahedra, the separating edges form the three parallel edges of a triangular prism - 96 triangular prisms, since the 24-cell contains 96 edges. Further, since each vertex was previously shared with 12 faces, the vertex would split into 12 (24*12=288) new vertices. Each group of 12 new vertices forms a cuboctahedron.
Coordinates
The Cartesian coordinates of the vertices of the cantellated 24-cell having edge length 2 are all permutations of coordinates and sign of:
- (0, √2, √2, 2+2√2)
- (1, 1+√2, 1+√2, 1+2√2)
The permutations of the second set of coordinates coincide with the vertices of an inscribed runcitruncated tesseract.
The dual configuration has all permutations and signs of:
- (0,2,2+√2,2+√2)
- (1,1,1+√2,3+√2)
Structure
The 24 small rhombicuboctahedra are joined to each other via their triangular faces, to the cuboctahedra via their axial square faces, and to the triangular prisms via their off-axial square faces. The cuboctahedra are joined to the triangular prisms via their triangular faces. Each triangular prism is joined to two cuboctahedra at its two ends.
Cantic snub 24-cell
A half-symmetry construction of the cantellated 24-cell, also called a cantic snub 24-cell, as ![]()
![]()
![]()
![]()
![]()
![]()
![]() , has an identical geometry, but its triangular faces are further subdivided. The cantellated 24-cell has 2 positions of triangular faces in ratio of 96 and 192, while the cantic snub 24-cell has 3 positions of 96 triangles.
, has an identical geometry, but its triangular faces are further subdivided. The cantellated 24-cell has 2 positions of triangular faces in ratio of 96 and 192, while the cantic snub 24-cell has 3 positions of 96 triangles.
The difference can be seen in the vertex figures, with edges representing faces in the 4-polytope:
 |
 |
Images
| Coxeter plane | F4 | |
|---|---|---|
| Graph |  | |
| Dihedral symmetry | [12] | |
| Coxeter plane | B3 / A2 (a) | B3 / A2 (b) |
| Graph | 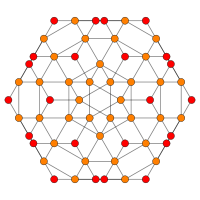 |
 |
| Dihedral symmetry | [6] | [6] |
| Coxeter plane | B4 | B2 / A3 |
| Graph |  |
 |
| Dihedral symmetry | [8] | [4] |
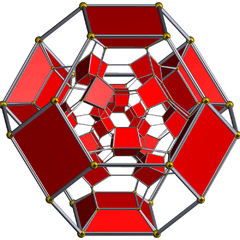
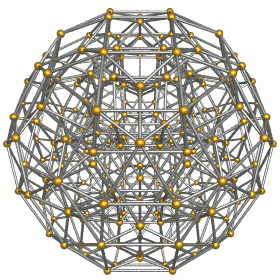 Schlegel diagram |
 Showing 24 cuboctahedra. |
 Showing 96 triangular prisms. |
Cantitruncated 24-cell
| Cantitruncated 24-cell | ||
|---|---|---|
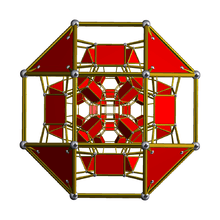
 Schlegel diagram, centered on truncated cuboctahedron | ||
| Type | Uniform 4-polytope | |
| Schläfli symbol | tr{3,4,3} | |
| Coxeter diagram | ||
| Cells | 144 | 24 4.6.8 96 4.4.3 24 3.8.8 |
| Faces | 720 | 192{3} 288{4} 96{6} 144{8} |
| Edges | 1152 | |
| Vertices | 576 | |
| Vertex figure | 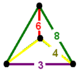 sphenoid | |
| Symmetry group | F4, [3,4,3] | |
| Properties | convex | |
| Uniform index | 27 28 29 | |
The cantitruncated 24-cell or great rhombated icositetrachoron is a uniform 4-polytope derived from the 24-cell. It is bounded by 24 truncated cuboctahedra corresponding with the cells of a 24-cell, 24 truncated cubes corresponding with the cells of the dual 24-cell, and 96 triangular prisms corresponding with the edges of the first 24-cell.
Coordinates
The Cartesian coordinates of a cantitruncated 24-cell having edge length 2 are all permutations of coordinates and sign of:
- (1,1+√2,1+2√2,3+3√2)
- (0,2+√2,2+2√2,2+3√2)
The dual configuration has coordinates as all permutations and signs of:
- (1,1+√2,1+√2,5+2√2)
- (1,3+√2,3+√2,3+2√2)
- (2,2+√2,2+√2,4+2√2)
Projections
| Coxeter plane | F4 | |
|---|---|---|
| Graph |  | |
| Dihedral symmetry | [12] | |
| Coxeter plane | B3 / A2 (a) | B3 / A2 (b) |
| Graph |  |
 |
| Dihedral symmetry | [6] | [6] |
| Coxeter plane | B4 | B2 / A3 |
| Graph | 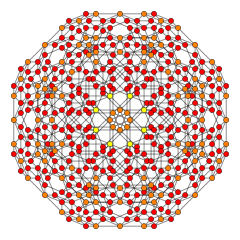 |
 |
| Dihedral symmetry | [8] | [4] |
 |
Related polytopes
| 24-cell family polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | 24-cell | truncated 24-cell | snub 24-cell | rectified 24-cell | cantellated 24-cell | bitruncated 24-cell | cantitruncated 24-cell | runcinated 24-cell | runcitruncated 24-cell | omnitruncated 24-cell | |
| Schläfli symbol |
{3,4,3} | t0,1{3,4,3} t{3,4,3} |
s{3,4,3} | t1{3,4,3} r{3,4,3} |
t0,2{3,4,3} rr{3,4,3} |
t1,2{3,4,3} 2t{3,4,3} |
t0,1,2{3,4,3} tr{3,4,3} |
t0,3{3,4,3} | t0,1,3{3,4,3} | t0,1,2,3{3,4,3} | |
| Coxeter diagram |
|||||||||||
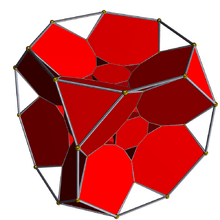
| Schlegel diagram |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| F4 |  |
 |
 |
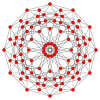 |
 |
 |
 |
 |
 |
 | |
| B4 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| B3(a) |  |
 |
 |
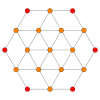 |
 |
 |
 |
 |
 |
 | |
| B3(b) |  |
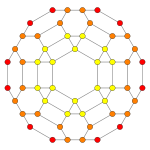 |
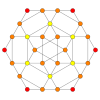 |
 |
 |
 | |||||
| B2 |  |
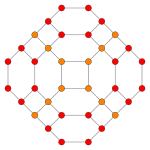 |
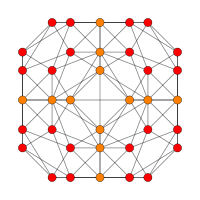 |
 |
 |
 |
 |
 |
 |
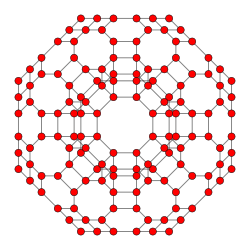 | |
References
- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- H.S.M. Coxeter:
- Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1n1)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- 3. Convex uniform polychora based on the icositetrachoron (24-cell) - Model 24, 25, George Olshevsky.
- Klitzing, Richard. "4D uniform polytopes (polychora)". x3o4x3o - srico, o3x4x3o - grico
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / E9 / E10 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||

