Reaction progress kinetic analysis

In chemistry, reaction progress kinetic analysis (RPKA) is a subset of a broad range of kinetic techniques utilized to determine the rate laws of chemical reactions and to aid in elucidation of reaction mechanisms. While the concepts guiding reaction progress kinetic analysis are not new, the process was formalized by Professor Donna Blackmond (currently at Scripps Research Institute) in the late 1990s and has since seen increasingly widespread use. Unlike more common pseudo-first-order analysis, in which an overwhelming excess of one or more reagents is used relative to a species of interest, RPKA probes reactions at synthetically relevant conditions (i.e. with concentrations and reagent ratios resembling those used in the reaction when not exploring the rate law.) Generally, this analysis involves a system in which the concentrations of multiple reactants are changing measurably over the course of the reaction. As the mechanism can vary depending on the relative and absolute concentrations of the species involved, this approach obtains results that are much more representative of reaction behavior under commonly utilized conditions than do traditional tactics. Furthermore, information obtained by observation of the reaction over time may provide insight regarding unexpected behavior such as induction periods, catalyst deactivation, or changes in mechanism.[1][2]

Monitoring reaction progress

Reaction progress kinetic analysis relies on the ability to accurately monitor the reaction conversion over time. This goal may be accomplished by a range of techniques, the most common of which are described below. While these techniques are sometimes categorized as differential (monitoring reaction rate over time) or integral (monitoring the amount of substrate and/or product over time), simple mathematical manipulation (differentiation or integration) allows interconversion of the data obtained by either of the two. Regardless of the technique implemented, it is generally advantageous to confirm the validity in the system of interest by monitoring with an additional independent method.[2]

Reaction progress NMR

NMR spectroscopy is often the method of choice for monitoring reaction progress, where substrate consumption and/or product formation may be observed over time from the change of peak integration relative to a non-reactive standard. From the concentration data, the rate of reaction over time may be obtained by taking the derivative of a polynomial fit to the experimental curve.[3] Reaction progress NMR may be classified as an integral technique as the primary data collected are proportional to concentration vs. time.[2] While this technique is extremely convenient for clearly defined systems with distinctive, isolated product and/or reactant peaks, it has the drawback of requiring a homogenous system amenable to reaction in an NMR tube. While NMR observation may allow for the identification of a reaction intermediates, the presence of any given species over the course of the reaction does not necessarily implicate it in a productive process.[1] Reaction progress NMR may, however, often be run at variable temperature, allowing the rate of reaction to be adjusted to a level convenient for observation. Examples of utilization of reaction progress NMR abound, with notable examples including investigation of Buchwald–Hartwig amination (One might note that considerable debate surrounded the best approach to mechanistic development of the Buchwald-Hartwig amination as indicated by a number of contradictory and competing reports published over a short period of time. See the designated article and references therein.)[4]

In situ FT-IR

In situ infrared spectroscopy may be used to monitor the course of a reaction, provided a reagent or product shows distinctive absorbance in the IR spectral region. The rate of reactant consumption and/or product formation may be abstracted from the change of absorbance over time (by application of Beers' Law). Even when reactant and product spectra display some degree of overlap, modern instrumentation software is generally able to accurately deconvolute the relative contributions provided there is a dramatic change in the absolute absorbance of the peak of interest over time. In situ IR may be classified as an integral technique as the primary data collected are proportional to concentration vs. time.[2] From these data, the starting material or product concentration over time may be obtained by simply taking the integral of a polynomial fit to the experimental curve.[3] With increases in the availability of spectrometers with in situ monitoring capabilities, FT-IR has seen increasing use in recent years. Examples of note include mechanistic analysis of the amido-thiourea catalyzed asymmetric Strecker synthesis of unnatural amino acids and of the Lewis base catalyzed halolactonization and cycloetherification.[5][6]

In situ UV-vis

Analogously to the in situ IR experiments described above, in situ UV-visible absorbance spectroscopy may be used to monitor the course of a reaction, provided a reagent or product shows distinctive absorbance in the UV spectral region. The rate of reactant consumption and/or product formation may be abstracted from the change of absorbance over time (by application of Beer's Law), again leading to classification as an integral technique.[2] Due to the spectral region utilized, UV-vis techniques are more commonly utilized on inorganic or organometallic systems than on purely organic reactions, and examples include exploration of the samarium Barbier reaction.[7]

Reaction calorimetry

Calorimetry may be used to monitor the course of a reaction, since the instantaneous heat flux of the reaction, which is directly related to the enthalpy change for the reaction, is monitored. Reaction calorimetry may be classified as a differential technique since the primary data collected are proportional to rate vs. time. From these data, the starting material or product concentration over time may be obtained by simply taking the integral of a polynomial fit to the experimental curve.[2][3][8] While reaction calorimetry is less frequently employed than a number of other techniques, it has found use as an effective tool for catalyst screening.[9] Reaction calorimetry has also been applied as an efficient method for mechanistic study of individual reactions including the prolinate-catalyzed α-amination of aldehydes,[10] and perhaps most notably, the palladium catalyzed Buchwald-Hartwig amination reaction.[4][11]

Further techniques

While Gas Chromatography, HPLC, and Mass Spectrometry are all excellent techniques for distinguishing mixtures of compounds (and sometimes even enantiomers), the time resolution of these measurements is less precise than that of the techniques described above. Regardless, these techniques have still seen use, such as in the investigation of the Heck reaction where the heterogeneous nature of the reaction precluded utilization of the techniques described above.[12] and SOMO-activation by organocatalysts[13] Despite their shortcomings, these techniques may serve as excellent calibration methods.

Data manipulation and presentation

a) The concentrations of substrate and/or product are monitored over time by methods such as in situ IR, UV-vis, or NMR or may be obtained by taking the integral of (c). b) Presenting the fractional conversion of substrate provides a normalization of the data in (a). c) The rate of reaction progress (product formation) is monitored over time by methods such as reaction progress calorimetry or may be obtained by taking the first derivative of (a). d) Describing the rate of reaction progress with respect to consumption of starting material spreads the data into a more informative distribution than observed in (c). Note that reaction progress is read from right (maximum substrate concentration) to left (no remaining substrate) in (d).

Reaction progress data may often most simply be presented as plot of substrate concentration ([A]t) vs. time (t) or fraction conversion (F) vs. time (t). The latter requires minor algebraic manipulation to convert concentration/absorbance values to fractional conversion (F), by:

F = [A]0 − [A]t/[A]0

where [A]0 is the amount, absorbance, or concentration of substrate initially present and [A]t is the amount, absorbance, or concentration of that reagent at time, t. Normalizing data to fractional conversion may be particularly helpful as it allows multiple reactions run with different absolute amounts or concentrations to be compared on the same plot.

Data may also commonly be presented as a plot of reaction rate (v) vs. time (t). Again, simple algebraic manipulation is required; for example, calorimetric experiments give:

v = q/VΔH

where q is the instantaneous heat transfer, ΔH is the known enthalpy change of the reaction, and V is the reaction volume.[2]

Data from reaction progress kinetics experiments are also often presented via a rate (v) vs. substrate concentration ([S]) plot. This requires obtaining and combining both the [S] vs. t and the v vs. t plots described above (note that one may be obtained from the other by simple differentiation or integration.) The combination leads to a standard set of curves in which reaction progress is read from right to left along the x-axis and reaction rate is read from bottom to top along the y-axis.[2] While these plots often provide a visually compelling demonstration of basic kinetic trends, differential methods are generally superior for extracting numerical rate constants. (see below)

Catalytic kinetics and catalyst resting state

In catalytic kinetics, two basic approximations are useful (in different circumstances) to describe the behavior of many systems. The situations in which the pre-equilibrium and steady-state approximations are valid can often be distinguished by reaction progress kinetic analysis, and the two situations are closely related to the resting state of the catalyst.

The steady-state approximation

a) The simplest case of steady state kinetics involves one substrate reversibly forming an intermediate complex (to which the steady-state approximation is applied) with the catalyst, followed by irreversible product formation. b) In a more complex example, two substrates bind the catalyst to sequentially form two intermediates (and the steady-state approximation is applied to both) followed by irreversible product formation. Note that because I2 is kinetically invisible, this is the same as for the case where I1 goes directly to free product and catalyst. For both (a) and (b), i) describes the catalytic cycle with relevant rate constants and concentrations, ii) displays the concentration of product and reactant over the course of the reaction, iii) describes the rate of the reaction as substrate is consumed from right to left, and iv) shows that the catalyst resting state is entirely the free catalyst while the concentrations of the intermediates remain small and approximately unchanging as substrate is consumed from right to left.

Under steady-state conditions, the catalyst and substrate undergo reversible association followed by a relatively rapid consumption of the catalyst–substrate complex (by both forward reactions to product and reverse reactions to unbound catalyst.) The steady-state approximation holds that the concentration of the catalyst-substrate complex is not changing over time; the total concentration of this complex remains low as it is whisked away almost immediately after formation. A steady-state rate law contains all of the rate constants and species required to go from starting material to product, while the denominator consists of a sum of terms describing the relative rates of the forward and reverse reactions consuming the steady-state intermediate. For the simplest case where one substrate goes to one product through a single intermediate:

d[P]/dt = k1k2[A][Cat]total/k−1 + k2

In a slightly more complex situation where two substrates bind in sequence followed by product release:

d[P]/dt = k1k2k3[A][B][Cat]total/(k−1 + k2[B])(k−2 + k3)[B]

Increasingly complex systems can be described simply with the algorithm described in this reference.[14]

In the case of the steady-state conditions described above, the catalyst resting state is the unbound form (because the substrate-bound intermediate is, by definition, only present at a minimal concentration.)

The pre-equilibrium approximation

a) The simplest case of pre-equilibrium kinetics involves one substrate rapidly and reversibly forming an intermediate complex with the catalyst, followed by irreversible product formation. b) In a more complex example, two substrates sequentially bind the catalyst rapidly and reversibly followed by irreversible product formation. For both (a) and (b), i) describes the catalytic cycle with relevant rate constants and concentrations, ii) displays the concentration of product and reactant over the course of the reaction, iii) describes the rate of the reaction as substrate is consumed from right to left, and iv) shows that the catalyst resting state is an equilibrium distribution of free catalyst and intermediates where the distribution is shifted increasingly toward free catalyst as substrate is consumed from right to left.

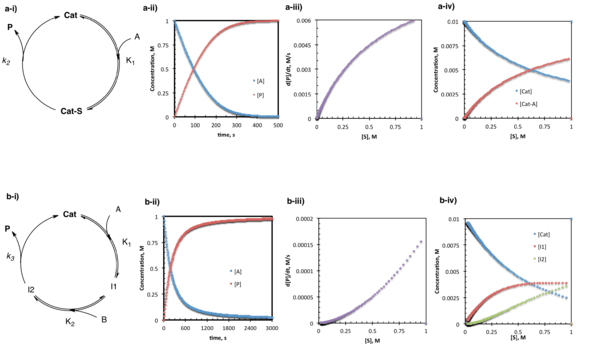
Under pre-equilibrium conditions, the catalyst and substrate undergo rapid and reversible association prior to a relatively slow step leading to product formation and release. Under these conditions, the system can be described by a "one-plus" rate law where the numerator consists of all rate constants and species required to go from starting material to product, and the denominator consists of a sum of terms describing each of the states in which the catalyst exists (and 1 corresponds to the free catalyst).[14] For the simplest case where one substrate goes to one product through a single intermediate:

d[P]/dt = K1k2[A][Cat]/1 + K1[A]

In the slightly more complex situation where two substrates bind in sequence followed by product release:

d[P]/dt = K1K2k2[A][B][Cat]/1 + K1[A] + K1K2[A][B]

In the case of the simple pre-equilibrium conditions described above, the catalyst resting state is either entirely or partially (depending on the magnitude of the equilibrium constant) the substrate bound complex.

Saturation kinetics

Saturation conditions can be viewed as a special case of pre-equilibrium conditions. At the concentration of substrate examined, formation of the catalyst-substrate complex is rapid and essentially irreversible. The catalyst resting state consists entirely of the bound complex, and [A] is no longer present in the rate law; changing [A] will have no effect on reaction rate because the catalyst is already completely bound and reacting as rapidly as k2 allows. The simplest case of saturation kinetics is the well-studied Michaelis-Menten model for enzyme kinetics.

Changes in catalyst resting state

a) The simplest case of saturation kinetics extends from the pre-equilibrium situation in which rapid substrate complexation with a catalyst is followed by slow formation of the product. b) The straight portion of the graph for substrate concentration over time is indicative of a zero-order dependence on substrate for most of the reaction, but the curve at low [A] is indicative of a change to (in this case) a first-order dependence on [A]. c) Saturation of the catalyst is apparent at high concentrations of substrate (where the rate has no dependence on [A], but as substrate is consumed, the reaction rate drops with a first-order dependence on [A] to pass through the origin. d) The catalyst resting state also changes, where it exists almost entirely as the substrate-bound complex, Cat–A, at high [A] but increasingly as the free catalyst, Cat, as [A] decreases over the course of the reaction.
The rate of product formation in the cyanosilylation of ketone, A, shows a slight non-linear dependence on catalyst loading at high catalyst concentrations. a) This observation, among others, is accounted for by the reversible formation of inactive catalyst complexes. b) Similar behavior at multiple conversion points is consistent with one dominant mechanism operating over the entire course of the reaction.[15]

While a reaction may exhibit one set of kinetic behavior at early conversion, that behavior may change due to:

In the case of saturation kinetics described above, provided that [A] is not present in a large excess relative to [B], saturation conditions will only apply at the beginning of the reaction. As the substrate is consumed, the concentration decreases and eventually [A] is no longer sufficient to completely overwhelm [Cat]. This is manifested by a gradual change in rate from 0-order to some higher (i.e. 1st, 2nd, etc.) order in [A]. This can also be described as a change in catalyst resting state from the bound form to the unbound form over the course of the reaction.

In addition to simply slowing the reaction, a change in catalyst resting state over the course of the reaction may result in competing paths or processes. Multiple mechanisms may be present to access the product, in which case the order in catalyst or substrate may change depending on the conditions or point in the reaction. A particularly useful probe for changes in reaction mechanism involves examination of the normalized reaction rate vs. catalyst loading at multiple, fixed conversion points. Note that the normalized reaction rate:

k = v/[A]t

adjusts for the consumption of substrate over the course of the reaction, so only rate changes due to catalyst loading will be observed. A linear dependence on catalyst loading for a given conversion is indicative of a first order dependence on catalyst at that conversion, and one can similarly imagine the non-linear plots resulting from higher order dependence. Changes in the linearity or non-linearity from one set of conversion points to another are indicative of changes in the dependence on catalyst over the course of the reaction. Conversely, changes in the linearity or non-linearity of regions of the plot conserved over multiple conversion points (i.e. at 30, 50, and 70%) are indicative of a change in the dependence on catalyst based on the absolute catalyst concentration.

Catalyst interactions with multiple components of a reaction mixture can lead to a complex kinetic dependence. While off-cycle catalyst-substrate or catalyst-product interactions are generally considered "poisonous" to the system (certainly the case in the event of irreversible complexation) cases do exist in which the off-cycle species actually protects the catalyst from permanent deactivation.[16][17] In either case, it is often essential to understand the role of the catalyst resting state.[3][10]

Same-excess experiments

The variable parameter of greatest interest in reaction progress kinetic analysis is the excess (e) of one substrate over another, given in units of molarity. The initial concentrations of two species in a reaction may be defined by:

[B]0 = [A]0 + e

and, assuming a one-to-one reaction stoichiometry, that excess of one substrate over the other is quantitatively preserved over the course of the entire reaction such that:[3]

[B]t = [A]t + e

A similar set can be constructed for reactions with higher order stoichiometry in which case the excess varies predictably over the course of the reaction. While e may be any value (positive, negative, or zero) generally positive or negative values smaller in magnitude than one equivalent of substrate are used in reaction progress kinetic analysis. (One might note that pseudo-zero-order kinetics uses excess values much much greater in magnitude than the one equivalent of substrate).

Defining the parameter of excess (e) allows for the construction of same-excess experiments in which two or more runs of a kinetic experiment with different initial concentrations, but the same-excess allow one to artificially enter the reaction at any point. These experiments are critical for RPKA of catalytic reactions, as they enable one to probe a number of mechanistic possibilities including catalyst activation (induction periods), catalyst deactivation, and product inhibition described in further detail below.[2][3]

Determining catalyst turnover frequency

Prior to further mechanistic investigation, it is important to determine the kinetic dependence of the reaction of interest on the catalyst. The turnover frequency (TOF) of the catalyst can be expressed as the reaction rate normalized to the concentration of catalyst:

TOF = v/[Cat]

This TOF is determined by running any two or more same-excess experiments in which the absolute catalyst concentration is varied. Because the catalyst concentration is constant over the course of the reaction, the resulting plots are normalized by an unchanging value. If the resulting plots overlay perfectly, then the reaction is, in fact, first-order in catalyst. If the reaction fails to overlay, higher-order processes are at work and require a more detailed analysis than described here.[3] It is also worth noting that the normalization-overlay manipulation described here is only one approach for interpretation of the raw data. Equally valid results may be obtained by fitting the observed kinetic behavior to simulated rate laws.

Exploring catalyst activation and deactivation

a) According to the proposed mechanism for the palladium-catalyzed amination of aryl halides, an induction period will be present as the active catalyst is generated from an inactive pre-catalyst (where L = BINAP). b) This induction period may be observed at early conversion points, before the catalyzed reaction reaches its maximum rate. In same-excess experiments, this will manifest itself in the non-overlying portions of curves designed to intercept the original reaction at intermediate conversion points. Here, a same-excess (e = 0.60 M) of [ArX] relative to [HNR2] and [MOR] is utilized for each of the curves.

As described above, same-excess experiments are conducted with two or more experiments holding the excess, (e) constant while changing the absolute concentrations of the substrates (in this case, the catalyst is also treated as a substrate.) Note that this construction causes the number of equivalents and therefore the mole percentage of each reagent/catalyst to differ between reactions.[3] These experiments enable one to artificially "enter" the reaction at any point, as the initial concentrations of one experiment (the intercepting reaction) are chosen to map directly onto the anticipated concentrations at some intermediate time, t, in another (the parent reaction). One would expect the reaction progress, described by the rate vs. substrate concentration plots detailed above, to map directly onto each other from that interception point onward. This will hold true, however, only if the rate of the reaction is not altered by changes to the active substrate/catalyst concentration (such as by catalyst activation, catalyst deactivation, or product inhibition) before that interception.[2][3]

A perfect overlay of multiple experiments with the same-excess but different initial substrate loadings suggests that no changes in the active substrate/catalyst concentration occur over the course of the reaction. The failure of the plots to overlay is generally indicative of catalyst activation, deactivation, or product inhibition under the reaction conditions. These cases may be distinguished by the position of the reaction progress curves relative to each other. Intercepting reactions lying below (slower rates at the same substrate concentration) the parent reactions on the rate vs. substrate concentration plot, are indicative of catalyst activation under reaction conditions. Intercepting reactions lying above (faster rates at the same substrate concentration) the parent reactions on the rate vs. substrate concentration plot, are indicative of catalyst deactivation under reaction conditions; further experimentation is necessary to distinguish product inhibition from other forms of catalyst death.[2]

One key difference between the intercepting reaction and the parent reaction described above is the presence of some amount of product in the parent reaction at the interception point. Product inhibition has long been known to influence catalyst efficiency of many systems, and in the case of same-excess experiments, it prevents the intercepting and parent reactions from overlaying. While same-excess experiments as described above cannot attribute catalyst deactivation to any particular cause, product inhibition can be probed by further experiments in which some initial amount of product is added to the intercepting reaction (designed to mimic the amount of product expected to be present in the parent reaction at the same substrate concentration.) A perfect overlay of the rate vs. substrate concentration plots under same-excess-same product conditions indicates that product inhibition does occur under the reaction conditions used. While the failure of the rate vs. substrate concentration plots to overlay under same-excess-same product conditions does not preclude product inhibition, it does, at least, indicate that other catalyst deactivation paths must also be active.

Reaction progress kinetic analysis can distinguish a) uninhibited catalysis b) irreversible catalyst death, and c) product inhibition by a series of same-excess experiments. Lack of overlay between rate vs. substrate concentration for multiple trials of the same reaction with the same-excess but different initial concentrations is indicative of product inhibition or catalyst death. The two may be distinguished where overlay of same-excess experiments with added product is indicative of product inhibition, where lack of overlay is indicative of an alternative form of catalyst death.

Same-excess experiments probing catalyst deactivation and product inhibition are among the most widely used applications of reaction progress kinetic analysis. Among the numerous examples in the literature, some include investigation of the amino alcohol-catalyzed zinc alkylation of aldehydes,[18] the amido-thiourea catalyzed asymmetric Strecker synthesis of unnatural amino acids,[5] and the SOMO-activation of organocatalysts.[13]

Determining reaction stoichiometry

Differential methods for extracting rate constants

With the wealth of data available from monitoring reaction progress over time paired with the power of modern computing methods, it has become reasonably straightforward to numerically evaluate the rate law, mapping the integrated rate laws of simulated reactions paths onto a fit of reaction progress over time. Due to the principles of the propagation of error, rate constants and rate laws can be determined by these differential methods with significantly lower uncertainty than by the construction of graphical rate equations (above.)[8]

Different-excess experiments

While RPKA allows observation of rates over the course of the entire reaction, conducting only same-excess experiments does not provide sufficient information for determination of the corresponding rate constants. In order to construct enough independent relationships to solve for all of the unknown rate constants, it is necessary to examine systems with different-excess.

Consider the simple example where the catalyst associates with substrate A, followed by reaction with B to form product, P and free catalyst. Regardless of the approximation applied, multiple independent parameters (k1, k−1, and k2 in the case of steady-state; k2 and K1 in the case of pre-equilibrium) are required to define the system. While one could imagine constructing multiple equations to describe the unknowns at different concentrations, when the data is obtained from a same-excess experiment [A] and [B] are not independent. Multiple experiments using different values of e are necessary to establish multiple independent equations defining the multiple independent rate constants in terms of experimental rates and concentrations. Non-linear least squares analysis may then be employed to obtain best fit values of the unknown rate constants to those equations.

Consider again the simple example discussed above where the catalyst associates with substrate A, followed by reaction with B to form product P and free catalyst. Regardless of the approximation applied, multiple independent parameters (k2 and K1 in the case of pre-equilibrium; k1, k−1, and k2 in the case of steady-state) are required to define the system. While one could imagine constructing multiple equations to describe the unknowns at different concentrations, when the data is obtained from a same-excess experiment [A] and [B] are not independent:

e = [B] − [A]

Multiple experiments using different values of e are necessary to establish multiple independent equations defining the multiple independent rate constants in terms of experimental rates and concentrations. Non-linear least squares analysis may then be employed to obtain best fit values of the unknown rate constants to those equations.

Graphical rate laws

One possible sequence for establishing kinetic order by reaction progress kinetic analysis. Adapted with modification from the process proposed by Donna Blackmond

Kineticists have historically relied on linearization of rate data to extrapolate rate constants, perhaps best demonstrated by the widespread use of the standard Lineweaver–Burke linearization of the Michaelis–Menten equation.[19] Linearization techniques were of particular importance before the advent of computing techniques capable of fitting complex curves, and they remain a staple in kinetics due to their intuitively simple presentation.[2] It is important to note that linearization techniques should NOT be used to extract numerical rate constants as they introduce a large degree of error relative to alternative numerical techniques. Graphical rate laws do, however, maintain that intuitive presentation of linearized data, such that visual inspection of the plot can provide mechanistic insight regarding the reaction at hand. The basis for a graphical rate law rests on the rate (v) vs. substrate concentration ([S]) plots discussed above. For example, in the simple cycle discussed with regard to different-excess experiments a plot of v/[A] vs. [B] and its twin v/[B] vs. [A] can provide intuitive insight about the order of each of the reagents. If plots of v/[A] vs. [B] overlay for multiple experiments with different-excess, the data are consistent with a first-order dependence on [A]. The same could be said for a plot of v/[A] vs. [A]; overlay is consistent with a first-order dependence on [B]. Non-overlaying results of these graphical rate laws are, of course, possible and are indicative of higher order dependence on the substrates probed. Blackmond has proposed a presenting the results of different-excess experiments with a series of graphical rate equations (that she presents in a flow-chart adapted here), but it is important to note that her proposed method is only one of many possible methods to display the kinetic relationship. Furthermore, while the presentation of graphical rate laws may at times be considered a visually simplified way to present complex kinetic data, fitting the raw kinetic data for analysis by differential or other rigorous numerical methods is necessary to extract accurate and quantitative rate constants and reaction orders.[2][3]

Reaction stoichiometry and mechanism

It is important to note that even while kinetic analysis is a powerful tool for determining the stoichiometry of the turn-over limiting transition state relative to the ground state, it cannot answer all mechanistic questions. It is possible for two mechanisms to be kinetically indistinguishable, especially under catalytic conditions. For any thorough mechanistic evaluation it is necessary to conduct kinetic analysis of both the catalytic process and its individual steps (when possible) in concert with other forms of analysis such as evaluation of linear free energy relationships, isotope effect studies, computational analysis, or any number of alternative approaches. Finally, it is important to note that no mechanistic hypothesis can ever be proven; alternative mechanistic hypothesis can only be disproven. It is, therefore, essential to conduct any investigation in a hypothesis-driven manner. Only by experimentally disproving reasonable alternatives can the support for a given hypothesis be strengthened.[20]

See also

References

  1. 1 2 Hartwig, J. F. (2010). Organotransition Metal Chemistry: From Bonding to Catalysis. Mill Valley, California: University Science Books. ISBN 978-1-891389-53-5.
  2. 1 2 3 4 5 6 7 8 9 10 11 12 13 Blackmond, D. G. (2005). "Reaction Progress Kinetic Analysis : A Powerful Methodology for Mechanistic Studies of Complex Catalytic Reactions". Angew. Chem. Int. Ed. 44: 4302–4320. doi:10.1002/anie.200462544.
  3. 1 2 3 4 5 6 7 8 9 10 Mathew, J. S.; Klussmann, M.; Iwamura, H.; Valera, F.; Futran, A,; Emanuelsson, E. A. C.; Blackmond, D. G. (1999). "Investigations of Pd-Catalyzed ArX Coupling Reactions Informed by Reaction Progress Kinetic Analysis". J. Org. Chem. 71: 4711–4722. doi:10.1021/jo052409i. Cite uses deprecated parameter |coauthors= (help)
  4. 1 2 Shekhar, S.; Ryberg, P.; Hartwig, J. F.; Mathew, J. S.; Blackmond, D. G.; Strieter, E. R.; Buchwald, S. L. (2006). "Reevaluation of the Mechanism of the Amination of Aryl Halides Catalyzed by BINAP-Ligated Palladium Complexes". J. Am. Chem. Soc. 128: 3584–3591. doi:10.1021/ja045533c.
  5. 1 2 Zuend, S. J.; Jacobsen, E. N. (2009). "Mechanism of Amido-Thiourea Catalyzed Enantioselective Imine Hydrocyanation: Transition State Stabilization via Multiple Non-Covalent Interactions". J. Am. Chem. Soc. 131: 15358–15374. doi:10.1021/ja9058958.
  6. ↑ Denmark, S. D.; Burk, M. T. (2010). "Lewis base catalysis of bromo- and iodolactonization, and cycloetherification". Proc. Natl. Acad. Sci. 107: 20655–20660. Bibcode:2010PNAS..10720655D. doi:10.1073/pnas.1005296107.
  7. ↑ Choquette, K. A.; Sadasivam, D. V.; Flowers, R. A. (2011). "Catalytic Ni(II) in Reactions of SmI2: Sm(II)- or Ni(0)-Based Chemistry?". J. Am. Chem. Soc. 133: 10655–10661. doi:10.1021/ja204287n.
  8. 1 2 Steel, C.; Naquvi, K. R. (1991). "Differential method in chemical kinetics". J. Phys. Chem. 95: 10703–10718. doi:10.1021/j100179a037.
  9. ↑ Blackmond, D. G.; Rosner, T.; Pfaltz, A. (1999). "Comprehensive Kinetic Screening of Catalysts Using Reaction Calorimetry". Org. Proc. Res. Dev. 3: 275–280. doi:10.1021/op990024u.
  10. 1 2 Hein, J. E.; Armstrong, A.; Blackmond, D. G. (2011). "Kinetic Profiling of Prolinate-Catalyzed α-Amination of Aldehydes". Org. Lett. 13: 4300–4303. doi:10.1021/ol201639z.
  11. ↑ Singh, U. K.; Strieter, E. R.; Blackmond, D. G.; Buchwald, S. L. (2002). "Mechanistic Insights into the Pd(BINAP)-Catalyzed Amination of Aryl Bromides:  Kinetic Studies under Synthetically Relevant Conditions". J. Am. Chem. Soc. 124: 14104–14114. doi:10.1021/ja026885r.
  12. ↑ Herrmann, W. A.; Brossmer, C.; Reisinger, C. P.; Riermeier, T. H.; Öfele, K.; Beller, M. (1997). "Palladacycles: Efficient New Catalysts for the Heck Vinylation of Aryl Halides". Chem. Eur. J. 3: 1357–1364. doi:10.1002/chem.19970030823.
  13. 1 2 Devery, J. J.; Conrad, J. C.; MacMillan, D. W. C.; Flowers, R. A. (2010). "Mechanistic Complexity in Organo–SOMO Activation". Angew. Chem. Int. Ed. 49: 6106–6110. doi:10.1002/anie.201001673.
  14. 1 2 Gilbert, H. F. (1977). ""Rule of thumb" for deriving steady state rate equations". J. Chem. Ed. 54: 492–493. Bibcode:1977JChEd..54..492G. doi:10.1021/ed054p492.
  15. ↑ The mechanistic scheme and kinetic data are adapted from independent kinetic simulations using the rate and equilibrium constants reported for the amino-thiourea catalyzed cyanosilylation of ketones by Zuend, S. J.; Jacobsen, E. N. J. Am. Chem. Soc. 2007, 129, 15872.
  16. ↑ List, B. (2002). "Proline-catalyzed asymmetric reactions". Tetrahedron. 58: 5573–5590. doi:10.1016/S0040-4020.
  17. ↑ Seebach, D.; Beck, A. K.; Badine, D. M.; Limbach, M.; Eschenmoser, A.; Treasurywala, A. M.; Hobi, R.; Prikoszovich, W. (2007). "Are Oxazolidinones Really Unproductive, Parasitic Species in Proline Catalysis? – Thoughts and Experiments Pointing to an Alternative View". Helv. Chim. Acta. 90: 425. doi:10.1002/hlca.200790050.
  18. ↑ Rosner, T.; Sears, P.J.; Nugent, W. A.; Blackmond. D.G. (2000). "Kinetic Investigations of Product Inhibition in the Amino Alcohol-Catalyzed Asymmetric Alkylation of Benzaldehyde with Diethylzinc". Org. Lett. 2: 2511–2513. doi:10.1021/ol006181r. Cite uses deprecated parameter |coauthors= (help)
  19. ↑ Lineweaver, H.; Burke, D. (1934). "The Determination of Enzyme Dissociation Constants". J. Am. Chem. Soc. 56: 658–666. doi:10.1021/ja01318a036.
  20. ↑ Platt, J. R. (1964). "Strong Inference". Science. 146: 347–353. Bibcode:1964Sci...146..347P. doi:10.1126/science.146.3642.347.
This article is issued from Wikipedia - version of the 11/7/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.