Kemeny–Young method

The Kemeny–Young method is a voting system that uses preferential ballots and pairwise comparison counts to identify the most popular choices in an election. It is a Condorcet method because if there is a Condorcet winner, it will always be ranked as the most popular choice.

This method assigns a score for each possible sequence, where each sequence considers which choice might be most popular, which choice might be second-most popular, which choice might be third-most popular, and so on down to which choice might be least-popular. The sequence that has the highest score is the winning sequence, and the first choice in the winning sequence is the most popular choice. (As explained below, ties can occur at any ranking level.)

The Kemeny–Young method is also known as the Kemeny rule, VoteFair popularity ranking, the maximum likelihood method, and the median relation.

Description

The Kemeny–Young method uses preferential ballots on which voters rank choices according to their order of preference. A voter is allowed to rank more than one choice at the same preference level. Unranked choices are usually interpreted as least-preferred.

Another way to view the ordering is that it is the one which minimizes the sum of the Kendall tau distances (bubble sort distance) to the voters' lists.

Kemeny–Young calculations are usually done in two steps. The first step is to create a matrix or table that counts pairwise voter preferences. The second step is to test all possible rankings, calculate a score for each such ranking, and compare the scores. Each ranking score equals the sum of the pairwise counts that apply to that ranking.

The ranking that has the largest score is identified as the overall ranking. (If more than one ranking has the same largest score, all these possible rankings are tied, and typically the overall ranking involves one or more ties.)

In order to demonstrate how an individual preference order is converted into a tally table, it is worth considering the following example. Suppose that a single voter has a choice among four candidates (i.e. Elliot, Meredith, Roland, and Selden) and has the following preference order:

Preference
order		 Choice
First Elliot
Second Roland
Third Meredith or Selden
(equal preference)

These preferences can be expressed in a tally table. A tally table, which arranges all the pairwise counts in three columns, is useful for counting (tallying) ballot preferences and calculating ranking scores. The center column tracks when a voter indicates more than one choice at the same preference level. The above preference order can be expressed as the following tally table.

All possible pairs
of choice names		 Number of votes with indicated preference
Prefer X over Y Equal preference Prefer Y over X
X = Selden
Y = Meredith		 0 +1 vote 0
X = Selden
Y = Elliot		 0 0 +1 vote
X = Selden
Y = Roland		 0 0 +1 vote
X = Meredith
Y = Elliot		 0 0 +1 vote
X = Meredith
Y = Roland		 0 0 +1 vote
X = Elliot
Y = Roland		 +1 vote 0 0

Now suppose that multiple voters had voted on those four candidates. After all ballots have been counted, the same type of tally table can be used to summarize all the preferences of all the voters. Here is an example for a case that has 100 voters.

All possible pairs
of choice names		 Number of votes with indicated preference
Prefer X over Y Equal preference Prefer Y over X
X = Selden
Y = Meredith		 50 10 40
X = Selden
Y = Elliot		 40 0 60
X = Selden
Y = Roland		 40 0 60
X = Meredith
Y = Elliot		 40 0 60
X = Meredith
Y = Roland		 30 0 70
X = Elliot
Y = Roland		 30 0 70


The sum of the counts in each row must equal the total number of votes.

After the tally table has been completed, each possible ranking of choices is examined in turn, and its ranking score is calculated by adding the appropriate number from each row of the tally table. For example, the possible ranking:

  1. Elliot
  2. Roland
  3. Meredith
  4. Selden

satisfies the preferences Elliot > Roland, Elliot > Meredith, Elliot > Selden, Roland > Meredith, Roland > Selden, and Meredith > Selden. The respective scores, taken from the table, are

giving a total ranking score of 30 + 60 + 60 + 70 + 60 + 40 = 320.

Calculating the overall ranking

After the scores for every possible ranking have been calculated, the ranking that has the largest score can be identified, and becomes the overall ranking. In this case, the overall ranking is:

  1. Roland
  2. Elliot
  3. Selden
  4. Meredith

with a ranking score of 370.

If there are cycles or ties, more than one possible ranking can have the same largest score. Cycles are resolved by producing a single overall ranking where some of the choices are tied.

Summary matrix

After the overall ranking has been calculated, the pairwise comparison counts can be arranged in a summary matrix, as shown below, in which the choices appear in the winning order from most popular (top and left) to least popular (bottom and right). This matrix layout does not include the equal-preference pairwise counts that appear in the tally table.

... over Roland ... over Elliot ... over Selden ... over Meredith
Prefer Roland ... - 70 60 70
Prefer Elliot ... 30 - 60 60
Prefer Selden ... 40 40 - 50
Prefer Meredith ... 30 40 40 -

[1]

In this summary matrix, the largest ranking score equals the sum of the counts in the upper-right, triangular half of the matrix (shown here in bold, with a green background). No other possible ranking can have a summary matrix that yields a higher sum of numbers in the upper-right, triangular half. (If it did, that would be the overall ranking.)

In this summary matrix, the sum of the numbers in the lower-left, triangular half of the matrix (shown here with a red background) are a minimum. The academic papers by John Kemeny and Peyton Young[2][3] refer to finding this minimum sum, which is called the Kemeny score, and which is based on how many voters oppose (rather than support) each pairwise order.

Method First-place winner
Kemeny–Young Roland
Condorcet Roland
Instant runoff voting Elliot or Selden
(depending on how the second-round tie is handled)
Plurality Selden

Example

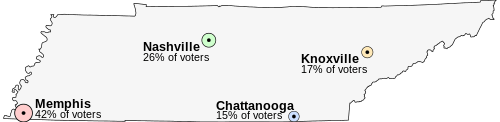
Tennessee and its four major cities: Memphis in the south-west; Nashville in the centre, Chattanooga in the south, and Knoxville in the east

Imagine that Tennessee is having an election on the location of its capital. The population of Tennessee is concentrated around its four major cities, which are spread throughout the state. For this example, suppose that the entire electorate lives in these four cities and that everyone wants to live as near to the capital as possible.

The candidates for the capital are:

The preferences of the voters would be divided like this:

42% of voters
(close to Memphis)		 26% of voters
(close to Nashville)		 15% of voters
(close to Chattanooga)		 17% of voters
(close to Knoxville)
  1. Memphis
  2. Nashville
  3. Chattanooga
  4. Knoxville
  1. Nashville
  2. Chattanooga
  3. Knoxville
  4. Memphis
  1. Chattanooga
  2. Knoxville
  3. Nashville
  4. Memphis
  1. Knoxville
  2. Chattanooga
  3. Nashville
  4. Memphis

This matrix summarizes the corresponding pairwise comparison counts:

... over
Memphis		 ... over
Nashville		 ... over
Chattanooga		 ... over
Knoxville
Prefer
Memphis ... 		- 42% 42% 42%
Prefer
Nashville ... 		58% - 68% 68%
Prefer
Chattanooga ... 		58% 32% - 83%
Prefer
Knoxville ... 		58% 32% 17% -


The Kemeny–Young method arranges the pairwise comparison counts in the following tally table:

All possible pairs
of choice names		 Number of votes with indicated preference
Prefer X over Y Equal preference Prefer Y over X
X = Memphis
Y = Nashville		 42% 0 58%
X = Memphis
Y = Chattanooga		 42% 0 58%
X = Memphis
Y = Knoxville		 42% 0 58%
X = Nashville
Y = Chattanooga		 68% 0 32%
X = Nashville
Y = Knoxville		 68% 0 32%
X = Chattanooga
Y = Knoxville		 83% 0 17%


The ranking score for the possible ranking of Memphis first, Nashville second, Chattanooga third, and Knoxville fourth equals (the unit-less number) 345, which is the sum of the following annotated numbers.

42% (of the voters) prefer Memphis over Nashville
42% prefer Memphis over Chattanooga
42% prefer Memphis over Knoxville
68% prefer Nashville over Chattanooga
68% prefer Nashville over Knoxville
83% prefer Chattanooga over Knoxville


This table lists all the ranking score .

First
choice 		Second
choice 		Third
choice 		Fourth
choice 		Ranking
score
Memphis Nashville Chattanooga Knoxville 345
Memphis Nashville Knoxville Chattanooga 279
Memphis Chattanooga Nashville Knoxville 309
Memphis Chattanooga Knoxville Nashville 273
Memphis Knoxville Nashville Chattanooga 243
Memphis Knoxville Chattanooga Nashville 207
Nashville Memphis Chattanooga Knoxville 361
Nashville Memphis Knoxville Chattanooga 295
Nashville Chattanooga Memphis Knoxville 377
Nashville Chattanooga Knoxville Memphis 393
Nashville Knoxville Memphis Chattanooga 311
Nashville Knoxville Chattanooga Memphis 327
Chattanooga Memphis Nashville Knoxville 325
Chattanooga Memphis Knoxville Nashville 289
Chattanooga Nashville Memphis Knoxville 341
Chattanooga Nashville Knoxville Memphis 357
Chattanooga Knoxville Memphis Nashville 305
Chattanooga Knoxville Nashville Memphis 321
Knoxville Memphis Nashville Chattanooga 259
Knoxville Memphis Chattanooga Nashville 223
Knoxville Nashville Memphis Chattanooga 275
Knoxville Nashville Chattanooga Memphis 291
Knoxville Chattanooga Memphis Nashville 239
Knoxville Chattanooga Nashville Memphis 255


The largest ranking score is 393, and this score is associated with the following possible ranking, so this ranking is also the overall ranking.

Preference
order		 Choice
First Nashville
Second Chattanooga
Third Knoxville
Fourth Memphis


If a single winner is needed, the first choice, Nashville, is chosen. (In this example Nashville is the Condorcet winner.)

The summary matrix below arranges the pairwise counts in order from most popular (top and left) to least popular (bottom and right).

... over Nashville ... ... over Chattanooga ... ... over Knoxville ... ... over Memphis ...
Prefer Nashville ... - 68% 68% 58%
Prefer Chattanooga ... 32% - 83% 58%
Prefer Knoxville ... 32% 17% - 58%
Prefer Memphis ... 42% 42% 42% -


In this arrangement the largest ranking score (393) equals the sum of the counts in bold, which are in the upper-right, triangular half of the matrix (with a green background).

Characteristics

In all cases that do not result in an exact tie, the Kemeny–Young method identifies a most-popular choice, second-most popular choice, and so on.

A tie can occur at any preference level. Except in some cases where circular ambiguities are involved, the Kemeny–Young method only produces a tie at a preference level when the number of voters with one preference exactly matches the number of voters with the opposite preference.

Satisfied criteria for all Condorcet methods

All Condorcet methods, including the Kemeny–Young method, satisfy these criteria:

Non-imposition
There are voter preferences that can yield every possible overall order-of-preference result, including ties at any combination of preference levels.
Condorcet criterion
If there is a choice that wins all pairwise contests, then this choice wins.
Majority criterion
If a majority of voters strictly prefer choice X to every other choice, then choice X is identified as the most popular.
Non-dictatorship
A single voter cannot control the outcome in all cases.

Additional satisfied criteria

The Kemeny–Young method also satisfies these criteria:

Unrestricted domain
Identifies the overall order of preference for all the choices. The method does this for all possible sets of voter preferences and always produces the same result for the same set of voter preferences.
Pareto efficiency
Any pairwise preference expressed by every voter results in the preferred choice being ranked higher than the less-preferred choice.
Monotonicity
If voters increase a choice's preference level, the ranking result either does not change or the promoted choice increases in overall popularity.
Smith criterion
The most popular choice is a member of the Smith set, which is the smallest nonempty set of choices such that every member of the set is pairwise preferred to every choice not in the Smith set.
Independence of Smith-dominated alternatives
If choice X is not in the Smith set, adding or withdrawing choice X does not change a result in which choice Y is identified as most popular.
Reinforcement
If all the ballots are divided into separate races and the overall ranking for the separate races are the same, then the same ranking occurs when all the ballots are combined.[4]
Reversal symmetry
If the preferences on every ballot are inverted, then the previously most popular choice must not remain the most popular choice.

Failed criteria for all Condorcet methods

In common with all Condorcet methods, the Kemeny–Young method fails these criteria (which means the described criteria do not apply to the Kemeny–Young method):

Independence of irrelevant alternatives
Adding or withdrawing choice X does not change a result in which choice Y is identified as most popular.
Invulnerability to burying
A voter cannot displace a choice from most popular by giving the choice an insincerely low ranking.
Invulnerability to compromising
A voter cannot cause a choice to become the most popular by giving the choice an insincerely high ranking.
Participation
Adding ballots that rank choice X over choice Y never cause choice Y, instead of choice X, to become most popular.
Later-no-harm
Ranking an additional choice (that was otherwise unranked) cannot displace a choice from being identified as the most popular.
Consistency
If all the ballots are divided into separate races and choice X is identified as the most popular in every such race, then choice X is the most popular when all the ballots are combined.

Additional failed criteria

The Kemeny–Young method also fails these criteria (which means the described criteria do not apply to the Kemeny–Young method):

Independence of clones
Offering a larger number of similar choices, instead of offering only a single such choice, does not change the probability that one of these choices is identified as most popular.
Invulnerability to push-over
A voter cannot cause choice X to become the most popular by giving choice Y an insincerely high ranking.
Schwartz
The choice identified as most popular is a member of the Schwartz set.
Polynomial runtime[5]
An algorithm is known to determine the winner using this method in a runtime that is polynomial in the number of choices.

Calculation methods and computational complexity

An algorithm for computing a Kemeny-Young ranking in time polynomial in the number of candidates is not known, and unlikely to exist since the problem is NP-hard[5] even if there are just 4 voters.[6][7]

It has been reported[8] that calculation methods based on integer programming sometimes allowed the computation of full rankings for votes on as many as 40 candidates in seconds. However, certain 40-candidate 5-voter Kemeny elections generated at random were not solvable on a 3 GHz Pentium computer in a useful time bound in 2006.[8]

Note that the complexity of computation scales linearly to the number of voters so the time needed to process a given set of votes is dominated by the number of candidates[9] rather than the number of votes, limiting the importance of this constraint to elections where voters are able to effectively consider significantly more than the common seven items of working memory.

There exists a polynomial-time approximation scheme for computing a Kemeny-Young ranking,[10] and there also exists a parameterized subexponential-time algorithm with running time O*(2O(√OPT)) for computing such a ranking.[11]

History

The Kemeny–Young method was developed by John Kemeny in 1959.[2]

In 1978 Peyton Young and Arthur Levenglick showed[3] that this method was the unique neutral method satisfying reinforcement and a version of the Condorcet criterion. In other papers,[12] [13] [14] [15] Young adopted an epistemic approach to preference-aggregation: he supposed that there was an objectively 'correct', but unknown preference order over the alternatives, and voters receive noisy signals of this true preference order (cf. Condorcet's jury theorem.) Using a simple probabilistic model for these noisy signals, Young showed that the Kemeny–Young method was the maximum likelihood estimator of the true preference order. Young further argues that Condorcet himself was aware of the Kemeny-Young rule and its maximum-likelihood interpretation, but was unable to clearly express his ideas.

In the papers by John Kemeny and Peyton Young, the Kemeny scores use counts of how many voters oppose, rather than support, each pairwise preference,[2][3] but the smallest such score identifies the same overall ranking.

Since 1991 the method has been promoted under the name "VoteFair popularity ranking" by Richard Fobes.[16]

See also

Notes

  1. ↑ The numbers in this example are adapted from .
  2. 1 2 3 John Kemeny, "Mathematics without numbers", Daedalus 88 (1959), pp. 577–591.
  3. 1 2 3 H. P. Young and A. Levenglick, "A Consistent Extension of Condorcet's Election Principle", SIAM Journal on Applied Mathematics 35, no. 2 (1978), pp. 285–300.
  4. ↑ Giuseppe Munda, "Social multi-criteria evaluation for a sustainable economy", p. 124.
  5. 1 2 J. Bartholdi III, C. A. Tovey, and M. A. Trick, "Voting schemes for which it can be difficult to tell who won the election", Social Choice and Welfare, Vol. 6, No. 2 (1989), pp. 157–165.
  6. ↑ C. Dwork, R. Kumar, M. Naor, D. Sivakumar. Rank Aggregation Methods for the Web, WWW10, 2001
  7. ↑ Biedl, Therese; Brandenburg, Franz J.; Deng, Xiaotie (2005-09-12). Healy, Patrick; Nikolov, Nikola S., eds. Crossings and Permutations. Lecture Notes in Computer Science. Springer Berlin Heidelberg. pp. 1–12. doi:10.1007/11618058_1. ISBN 9783540314257.
  8. 1 2 Vincent Conitzer, Andrew Davenport, and Jayant Kalagnanam, "Improved bounds for computing Kemeny rankings" (2006).
  9. ↑
  10. ↑ "How to Rank with Few Errors". http://cs.brown.edu/~claire/stoc07.pdf
  11. ↑ Karpinski, M. and Schudy, W., "Faster Algorithms for Feedback Arc Set Tournament, Kemeny Rank Aggregation and Betweenness Tournament", in: Cheong, O., Chwa, K.-Y., and Park, K. (Eds.): ISAAC 2010, Part I, LNCS 6506, pp. 3-14.
  12. ↑ H. P. Young, "Condorcet's Theory of Voting", American Political Science Review 82, no. 2 (1988), pp. 1231–1244.
  13. ↑ H. P. Young, "Optimal ranking and choice from pairwise comparisons", in Information pooling and group decision making edited by B. Grofman and G. Owen (1986), JAI Press, pp. 113–122.
  14. ↑ H. P. Young, "Optimal Voting Rules", Journal of Economic Perspectives 9, no.1 (1995), pp. 51–64.
  15. ↑ H. P. Young, "Group choice and individual judgements", Chapter 9 of Perspectives on public choice: a handbook, edited by Dennis Mueller (1997) Cambridge UP., pp.181 –200.
  16. ↑ Richard Fobes, "The Creative Problem Solver's Toolbox", (ISBN 0-9632-2210-4), 1993, pp. 223–225.

External links

This article is issued from Wikipedia - version of the 10/13/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.