ISO 216

ISO 216 specifies international standard (ISO) paper sizes used in most countries in the world today, although not in Canada or the United States. The standard defines the "A" and "B" series of paper sizes, including A4, the most commonly available size. Two supplementary standards, ISO 217 and ISO 269, define related paper sizes; the ISO 269 "C" series is commonly listed alongside the A and B sizes.

All ISO 216, ISO 217 and ISO 269 paper sizes (except some envelopes) have the same aspect ratio, 1:√2, at least to within the rounding to whole numbers of millimetres. This ratio has the unique property that when cut or folded in half widthwise, the halves also have the same aspect ratio. Each ISO paper size is one half of the area of the next larger size.

Dimensions of A, B and C Series

ISO/DIN paper sizes in millimetres and in inches
Size	A series formats		B series formats		C series formats
Size	(mm)	(in)	(mm)	(in)	(mm)	(in)
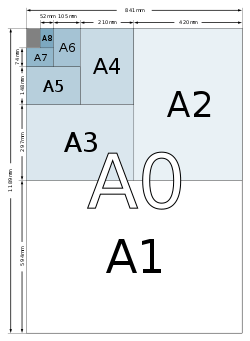
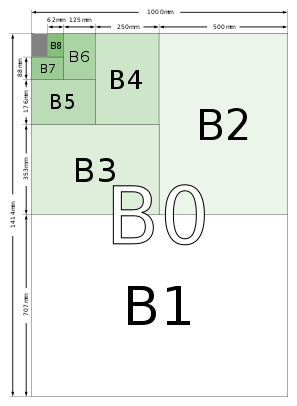
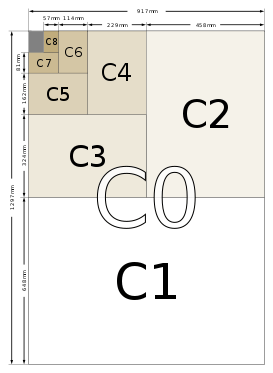
0	841 × 1189	33.1 × 46.8	1000 × 1414	39.4 × 55.7	917 × 1297	36.1 × 51.1
1	594 × 841	23.4 × 33.1	707 × 1000	27.8 × 39.4	648 × 917	25.5 × 36.1
2	420 × 594	16.5 × 23.4	500 × 707	19.7 × 27.8	458 × 648	18.0 × 25.5
3	297 × 420	11.7 × 16.5	353 × 500	13.9 × 19.7	324 × 458	12.8 × 18.0
4	210 × 297	8.3 × 11.7	250 × 353	9.8 × 13.9	229 × 324	9.0 × 12.8
5	148 × 210	5.8 × 8.3	176 × 250	6.9 × 9.8	162 × 229	6.4 × 9.0
6	105 × 148	4.1 × 5.8	125 × 176	4.9 × 6.9	114 × 162	4.5 × 6.4
7	74 × 105	2.9 × 4.1	88 × 125	3.5 × 4.9	81 × 114	3.2 × 4.5
8	52 × 74	2.0 × 2.9	62 × 88	2.4 × 3.5	57 × 81	2.2 × 3.2
9	37 × 52	1.5 × 2.0	44 × 62	1.7 × 2.4	40 × 57	1.6 × 2.2
10	26 × 37	1.0 × 1.5	31 × 44	1.2 × 1.7	28 × 40	1.1 × 1.6

Comparison of ISO 216 paper sizes between A4 and A3 and Swedish extension SIS 014711 sizes.

History

"Lichtenberg ratio" redirects here. For √2, see Square root of 2.

In 1786, the German scientist Georg Christoph Lichtenberg described the advantages of basing a paper size on an aspect ratio of ${\sqrt {2}}$ in a letter to Johann Beckmann.^[1] The formats that became ISO paper sizes A2, A3, B3, B4, and B5 were developed in France. They were listed in a 1798 law on taxation of publications that was based in part on page sizes.^[2]

Comparison of A4 (shaded grey) and C4 sizes with some similar paper and photographic paper sizes.

The main advantage of this system is its scaling. Rectangular paper with an aspect ratio of ${\sqrt {2}}$ has the unique property that, when cut or folded in half midway between its shorter sides, each half has the same ${\sqrt {2}}$ aspect ratio and half the area of the whole sheet before it was divided. Equivalently, if one lays two same-sized sheets paper with an aspect ratio of ${\sqrt {2}}$ side-by-side along their longer side, they form a larger rectangle with the aspect ratio of ${\sqrt {2}}$ and double the area of each individual sheet.

The ISO system of paper sizes exploit these properties of the ${\sqrt {2}}$ aspect ratio. In each series of sizes (for example, series A), the largest size is numbered 0 (for example, A0), and each successive size (for example, A1, A2, etc.) has half the area of the preceding sheet and can be cut by halving the length of the preceding size sheet. A folded brochure can be made by using a sheet of the next larger size (for example, an A4 sheet is folded in half to make a brochure with size A5 pages. An office photocopier or printer can be designed to reduce a page from A4 to A5 or to enlarge a page from A4 to A3. Similarly, two sheets of A4 can be scaled down to fit one A4 sheet without excess empty paper.

This system also simplifies calculating the weight paper. Under ISO 536, paper's grammage is defined as a sheet's weight in grams (g) per area in square metres (abbreviated g/m² or gsm).^[3] Since an A0 sheet has an area of 1 m², its weight in grams is the same as its grammage. One can derive the grammage of other sizes by arithmetic division in g/m². A standard A4 sheet made from 80 g/m² paper weighs 5 g, as it is ¹⁄₁₆ (four halvings, ignoring roundings to exact mm) of an A0 page. Thus the weight, and the associated postage rate, can be easily approximated by counting the number of sheets used.

ISO 216 and its related standards were first published between 1975 and 1995:

ISO 216:2007, defining the A and B series of paper sizes
ISO 269:1985, defining the C series for envelopes
ISO 217:2013, defining the RA and SRA series of raw ("untrimmed") paper sizes

A series

Paper in the A series format has a $\sqrt{2} \approx 1.414$ aspect ratio, rounded to the nearest millimetre. A0 is defined so that it has an area of 1 square metre before rounding. Successive paper sizes in the series (A1, A2, A3, etc.) are defined by halving the length of the preceding paper size, so that the long side of ${\text{A}}(n+1)$ is the same length as the short side of ${\text{A}}n$ before rounding.

The most frequently used of this series is the size A4 which is 210 mm × 297 mm (8.27 in × 11.7 in) and so almost ${\frac {1}{16}}$ square metres in area. For comparison, the letter paper size commonly used in North America (8.5 in × 11 in (216 mm × 279 mm)) is approximately 6 mm (0.24 in) wider and 18 mm (0.71 in) shorter than A4.

The geometric rationale behind the square root of 2 is to maintain the aspect ratio of each subsequent rectangle after cutting or folding an A series sheet in half, perpendicular to the larger side. Given a rectangle with a longer side, x, and a shorter side, y, ensuring that its aspect ratio, ${\frac {x}{y}}$ , will be the same as that of a rectangle half its size, ${\frac {y}{x/2}}$ , means that ${\frac {x}{y}}={\frac {y}{x/2}}$ , which reduces to ${\frac {x}{y}}={\sqrt {2}}$ ; in other words, an aspect ratio of $1:\sqrt{2}$ .

The formula that gives the larger border of the paper size An in metres and without rounding off is the geometric sequence: $a_{n}=2^{{\frac {1}{4}}-{\frac {n}{2}}}$ . The paper size An thus has the dimension $a_{n}\times a_{n+1}$ and area (before rounding off) $2^{-n}\mathrm {m} ^{2}$ .

The exact millimetre measurement of the long side of An is given by $\left\lfloor 1000/\left(2^{\frac {2n-1}{4}}\right)+0.2\right\rfloor$ , in which the modified brackets represent the floor function.

B series

The B series is defined in the standard as follows: "A subsidiary series of sizes is obtained by placing the geometrical means between adjacent sizes of the A series in sequence." The use of the "geometric means", means that each step in size: B0, A0, B1, A1, B2 … is smaller than the previous by an equal scaling. As with the A series, the lengths of the B series have the ratio 1:√2, and folding one in half gives the next in the series. The shorter side of B0 is exactly 1 metre.

There is also an incompatible Japanese B series which the JIS defines to have 1.5 times the area of the corresponding JIS A series (which is identical to the ISO A series).^[4] Thus, the lengths of JIS B series paper are $\sqrt{1.5} \approx 1.22$ times those of A-series paper. By comparison, the lengths of ISO B series paper are $\sqrt[4]{2} \approx 1.19$ times those of A-series paper.

For the ISO B series, the exact millimetre measurement of the long side of Bn is given by $\left\lfloor 1000/\left(2^{\frac {n-1}{2}}\right)+0.2\right\rfloor$ .

C series

The C series formats are geometric means between the B series and A series formats with the same number (e.g., C2 is the geometric mean between B2 and A2). The width to height ratio is as in the A and B series. The C series formats are used mainly for envelopes. An A4 page will fit into a C4 envelope. C series envelopes follow the same ratio principle as the A series pages. For example, if an A4 page is folded in half so that it is A5 in size, it will fit into a C5 envelope (which will be the same size as a C4 envelope folded in half). The lengths of ISO C series paper are therefore ⁸√2 times those of A-series paper – i.e., about 9% larger.

A, B, and C paper fit together as part of a geometric progression, with ratio of successive side lengths of ⁸√2, though there is no size half-way between Bn and A(n − 1): A4, C4, B4, "D4", A3, …; there is such a D-series in the Swedish extensions to the system.

The exact millimetre measurement of the long side of Cn is given by $\left\lfloor 1000/\left(2^{\frac {4n-3}{8}}\right)+0.2\right\rfloor$ .

Tolerances

The tolerances specified in the standard are:

±1.5 mm for dimensions up to 150 mm,
±2.0 mm for dimensions in the range 150 to 600 mm, and
±3.0 mm for dimensions above 600 mm.

These are related to comparison between series A, B and C.

Application

The ISO 216 formats are organized around the ratio 1:√2; two sheets next to each other together have the same ratio, sideways. In scaled photocopying, for example, two A4 sheets reduced to A5 size fit exactly onto one A4 sheet, and an A4 sheet in magnified size onto an A3 sheet; in each case, there is neither waste nor want.

The principal countries not generally using the ISO paper sizes are the United States and Canada, which use the Letter, Legal and Executive system. Although they have also officially adopted the ISO 216 paper format, Mexico, Panama, Venezuela, Colombia, the Philippines, and Chile also use mostly U.S. paper sizes.

Rectangular sheets of paper with the ratio 1:√2 are popular in paper folding, such as origami, where they are sometimes called "A4 rectangles" or "silver rectangles".^[5] In other contexts, the term "silver rectangle" can also refer to a rectangle in the proportion 1:(1 + √2), known as the silver ratio.

References

↑ Lichtenberg, Georg Christoph (February 7, 2006) [Written October 25, 1786]. "Lichtenberg's letter to Johann Beckmann" (in German with English translation). Translated by Kuhn, Markus. University of Cambridge. Retrieved May 10, 2016. Published in Lichtenberg, Georg Christoph (1990). Joost, Ulrich; Schöne, Albrecht, eds. Briefwechsel [Correspondence] (in German). Volume III (1785-1792). Munich: Beck. pp. 274–75. ISBN 3-406-30958-5. Retrieved May 10, 2016.
↑ Kuhn, Markus (October 8, 2005). "Loi sur le timbre (No. 2136)" [Law of Taxation (No. 2136)]. Retrieved May 11, 2016. Kuhn includes copies of pages from the journal article that announced the law: Republic of France (November 3, 1798). "Loi sur le timbre (Nº 2136)". Bulletin des lois de la République (in French). Paris (237): 1–2.
↑ International Organization for Standardization (2012). "ISO 536:2012(en): Paper and board — Determination of grammage". ISO Browsing Platform (3 ed.). § 3.1 note 1. Missing or empty |url= (help)
↑ "Japanese B Series Paper Size". Retrieved 2010-04-18.
↑ Lister, David. "The A4 rectangle". The Lister List. England: British Origami Society. Retrieved 2009-05-06.

External links

Wikimedia Commons has media related to DIN EN ISO 216.

International standard paper sizes: ISO 216 details and rationale
ISO 216 at iso.org

ISO standards by standard number

List of ISO standards / ISO romanizations / IEC standards

1–9999	1 2 3 4 5 6 7 9 16 31 -0 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10 -11 -12 -13 128 216 217 226 228 233 259 269 302 306 428 518 519 639 -1 -2 -3 -5 -6 646 690 732 764 843 898 965 1000 1004 1007 1073-1 1413 1538 1745 1989 2014 2015 2022 2047 2108 2145 2146 2240 2281 2709 2711 2788 2852 3029 3103 3166 -1 -2 -3 3297 3307 3602 3864 3901 3977 4031 4157 4217 4909 5218 5428 5775 5776 5800 5964 6166 6344 6346 6385 6425 6429 6438 6523 6709 7001 7002 7098 7185 7200 7498 7736 7810 7811 7812 7813 7816 8000 8178 8217 8571 8583 8601 8632 8652 8691 8807 8820-5 8859 -1 -2 -3 -4 -5 -6 -7 -8 -8-I -9 -10 -11 -12 -13 -14 -15 -16 8879 9000/9001 9075 9126 9293 9241 9362 9407 9506 9529 9564 9594 9660 9897 9899 9945 9984 9985 9995

10000–19999	10005 10006 10007 10116 10118-3 10160 10161 10165 10179 10206 10218 10303 -11 -21 -22 -28 -238 10383 10487 10585 10589 10646 10664 10746 10861 10957 10962 10967 11073 11170 11179 11404 11544 11783 11784 11785 11801 11898 11940 (-2) 11941 11941 (TR) 11992 12006 12182 12207 12234-2 13211 -1 -2 13216 13250 13399 13406-2 13450 13485 13490 13567 13568 13584 13616 14000 14031 14224 14289 14396 14443 14496 -2 -3 -6 -10 -11 -12 -14 -17 -20 14644 14649 14651 14698 14750 14764 14882 14971 15022 15189 15288 15291 15292 15398 15408 15444 -3 15445 15438 15504 15511 15686 15693 15706 -2 15707 15897 15919 15924 15926 15926 WIP 15930 16023 16262 16612-2 16750 16949 (TS) 17024 17025 17203 17369 17442 17799 18000 18004 18014 18245 18629 18916 19005 19011 19092 (-1 -2) 19114 19115 19125 19136 19439 19500 19501 19502 19503 19505 19506 19507 19508 19509 19510 19600:2014 19752 19757 19770 19775-1 19794-5 19831

20000+	20000 20022 20121 21000 21047 21500 21827:2002 22000 23270 23271 23360 24517 24613 24617 24707 25178 25964 26000 26300 26324 27000 series 27000 27001:2005 27001:2013 27002 27006 27729 28000 29110 29148 29199-2 29500 30170 31000 32000 38500 40500 42010 80000 -1 -2 -3

Category

Deutsches Institut für Normung

DIN standards	DIN 1025 DIN 1451 DIN 1530 DIN 5008 DIN 31635 DIN 41612 DIN 43700 DIN 4420 DIN 47100 DIN 62056 DIN 72552 Engschrift ISO 216

Committees	Municipal Services Standards Committee

Connectors	DIN connector Mini-DIN connector Multimedia extension connector

Rails	DIN rail

This article is issued from Wikipedia - version of the 11/21/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.