Viviani's curve
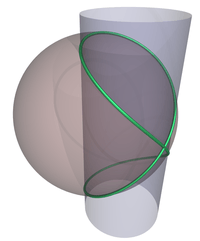
Viviani's curve as intersection of a sphere and a cylinder
In mathematics, particularly geometry, Viviani's curve, also known as Viviani's window, is a figure eight shaped space curve named after the Italian mathematician Vincenzo Viviani, the intersection of a sphere with a cylinder that is tangent to the sphere and passes through the center of the sphere.
The projection of Viviani's curve onto a plane perpendicular to the line through the crossing point and the sphere center is the lemniscate of Gerono.[1]
Formula
The curve can be obtained by intersecting a sphere of radius centered at the origin,
with the cylinder centered at of radius given by
The resulting curve of intersection, , can be parameterized by to give the parametric equation of Viviani's curve:
This is a clelie with , where .
See also
References
- ↑ Costa, Luisa Rossi; Marchetti, Elena (2005), "Mathematical and Historical Investigation on Domes and Vaults", in Weber, Ralf; Amann, Matthias Albrecht, Aesthetics and architectural composition : proceedings of the Dresden International Symposium of Architecture 2004, Mammendorf: Pro Literatur, pp. 73–80.
External links
- Hazewinkel, Michiel, ed. (2001), "Viviani curve", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Weisstein, Eric W. "Viviani's Curve". MathWorld.
This article is issued from Wikipedia - version of the 7/14/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.