Perceived visual angle

In human visual perception, the visual angle, denoted θ, subtended by a viewed object sometimes looks larger or smaller than its actual value. One approach to this phenomenon posits a subjective correlate to the visual angle: the perceived visual angle or perceived angular size. An optical illusion where the physical and subjective angles differ is then called a visual angle illusion or angular size illusion.

Angular size illusions are most obvious as relative angular size illusions, in which two objects that subtend the same visual angle appear to have different angular sizes; it is as if their equal-sized images on the retina were of different sizes. Angular size illusions are contrasted with linear size illusions, in which two objects that are the same physical size do not appear so. An angular size illusion may be accompanied by (or cause) a linear size illusion at the same time.

The perceived visual angle paradigm begins with a rejection of the classical size–distance invariance hypothesis (SDIH), which states that the ratio of perceived linear size to perceived distance is a simple function of the visual angle. The SDIH does not explain some illusions, such as the Moon illusion, in which the Moon appears larger when it is near the horizon. It is replaced by a perceptual SDIH, in which the visual angle is replaced by the perceived visual angle. This new formulation avoids some of the paradoxes of the SDIH, but it remains difficult to explain why a given illusion occurs.

This paradigm is not universally accepted; many textbook explanations of size and distance perception do not refer to the perceived visual angle, and some researchers deny that it exists. Some recent evidence supporting the idea, reported by Murray, Boyaci and Kersten (2006), suggests a direct relationship between the perceived angular size of an object and the size of the neural activity pattern it excites in the primary visual cortex.

A relatively new idea

Visual angle illusions have been explicitly described by many vision researchers, including Joynson (1949), (McCready 1963, 1965, 1985, 1999), Rock & McDermott (1964), Baird (1970), Ono (1970), Roscoe (1985, 1989), Hershenson (1982, 1989), Reed (1984, 1989), Enright (1989), Plug & Ross (1989, 1994), Higashiyama & Shimono (1994), Gogel, & Eby (1997), Ross & Plug (2002), and Murray, Boyaci & Kersten (2006). Specifically, these researchers cited have advocated a relatively new idea: that many of the best-known size illusions demonstrate that for most observers the (subjective) perceived visual angle, θ′, can change for a viewed target that subtends a constant (physical) visual angle θ.

Indeed, various experiments have revealed most of the factors responsible for these visual angle illusions, and a few different explanations for them have been published (Baird, Wagner, & Fuld, 1990, Enright, 1987, 1989, Hershenson, 1982, 1989, Komoda & Ono, 1974, McCready, 1965, 1985, 1986, 1994, Ono, 1970, Oyama, 1977, Reed, 1984, 1989, Restle, 1970, Roscoe, 1985, 1989).

On the other hand, nearly all discussions (and explanations) of those classic size illusions found in textbooks, the popular media, and on the internet use, instead, an older hypothesis that the visual angle is not perceivable (Gregory, 2008, Kaufman & Kaufman, 2002). They can describe and explain only a linear size illusion, which is why they do not properly describe or explain the illusions that most people experience.

In order to clarify the new paradigm which replaces the old one, it helps to keep in mind that an angle is the difference between two directions from a common point (the vertex). Accordingly, as described below, the visual angle θ is the difference between two real (optical) directions in the field of view, while the perceived visual angle θ′, is the difference by which the directions of two viewed points from oneself appear to differ in the visual field.

Physical measures S, D, R, and θ

Figure 1 illustrates an observer's eye looking at a frontal extent AB that has a linear size S (also called its "metric size" or "tape-measure size"). The extent's lower endpoint at B lies at a distance D from point O, which for present purposes can represent the center of the eye's entrance pupil.

The line from B through O indicates the chief ray of the bundle of light rays that form the optical image of B on the retina at point b, let's say, on the fovea. Likewise, endpoint A is imaged at point a.

The optical (physical) angle between those chief rays is the visual angle θ which can be calculated:

The retinal images at b and a are separated by the distance R, given by the equation

in which n is the eye's nodal distance that averages about 17 mm. That is, a viewed object's retinal image size is approximately given by R = 17 S/D mm.

The line from point O outward through object point B specifies the optical direction, d_B, of the object's base from the eye, let's say toward the horizon. The line from point O through point A specifies that endpoint's optical direction, d_A, toward some specific elevation value (say, 18 degrees). The difference between those real directions (d_A − d_B) is, again, the visual angle θ.

Perceived measures

Figure 2 diagrams the perceived (subjective) values for a viewed object.

Point O′ represents the place from which the observer feels that he or she is viewing the world. For present purposes, O′ can represent the cyclopean eye (Ono, 1970, Ono, Mapp & Howard, 2002).^[1]

Perceived linear values D′ and S′

In Figure 2, D′ is the perceived distance of the subjective point B′ from O′. The observer might simply say how far away point B′ looks, in inches or meters or miles.

Similarly, S′ is the perceived linear extent by which the subjective point A′ appears directly above point B′. The observer could simply say how many inches or meters that vertical distance looks. For a viewed object, S′ thus is its perceived linear size in meters, (or apparent linear size).

Perceived visual angle θ′

The perceived endpoint at B′ has the perceived direction, d′_B, and the observer might simply say "it looks straight ahead and toward the horizon."

This concept of the (subjective) visual direction is very old.^[2] However, as Wade, Ono & Mapp (2006) noted, it unfortunately has been ignored in many current theories of size perception, and size illusions.

The object's other perceived endpoint, A′, has a perceived direction d′_A;, about which the observer might say "it appears toward a higher elevation than point B′." The difference between the two perceived directions (d′_A − d′_B) is the perceived visual angle θ′, also called the perceived angular size or apparent angular size.

It is not easy to quantify θ′. For instance, a well-trained observer might say that point A′ "looks about 25 degrees higher" than B′, but most cannot reliably say how large a direction difference looks. That skill is not practiced because it is easier to use pointing gestures (Ono, 1970): For example, one often tells another person about the change in the directions seen for two viewed points by pointing something, say a finger or the eyes from one point to the other.

Therefore, in some experiments the observers aimed a pointer from one viewed point to the other, so the angle through which the pointer rotated was the measure of θ′, (Komodo, 1970, Komodo & Ono, 1974, Ono, Muter, & Mitson, 1974, Gogel & Eby, 1997).

Also, because θ′, specifies the amount by which one should rotate one's eye to quickly look from one seen point to another eye tracking, saccade, observers in other experiments shifted their gaze from one object endpoint to the other, and the angle the eye rotated through was measured as θ′ for that object (Yarbus (1967).

Difference between θ′ and S′

It is important to understand how θ′ differs from S′. Consider an example illustrated by the sketch at the right.

Suppose one is looking through a window at a 30-foot-wide (9.1 m) house 240 feet away, so it subtends a visual angle of about 7 degrees. The 30-inch-wide (760 mm) window opening is 10 feet away, so it subtends a visual angle of 14 degrees.

It can be said that the house "looks larger and farther away" than the window, meaning that the perceived linear size S′ for the house's width is much larger than S′ for the window; for instance a person might say the house "looks about 40 feet wide" and the window "looks about 3 feet wide."

One can also say that the house "looks smaller and farther away" than the window, and that does not contradict the other statement because now we mean that the amount (θ′) by which directions of the house's edges appear to differ is, say, about half the apparent direction difference for the window edges.

Notice that humans experience both the linear size and the angular size comparisons at the same time, along with the distance comparison (Joynson, 1949). Thus any report merely that one object "looks larger" than another object is ambiguous. It needs to specify whether "looks larger" refers to the perceived angular size (θ′) or to the perceived linear size (S′) or to both of those qualitatively different "size" experiences (Joynson, 1949, McCready, 1965, 1985, Ono, 1970). Notice that in everyday conversations "looks larger" often refers to an angular size comparison rather than a linear size comparison.

Additional confusion has resulted from widespread use of the ambiguous terms "apparent size" and "perceived size", because they sometimes have referred to θ′ and sometimes to S′ without clarification, so the reader must try to ascertain what they mean. Also, in astronomy, "apparent size" refers to the physical angle θ rather than to the subjective apparent visual angle θ′.

The perceptual size–distance invariance hypothesis

How the three perceived values θ′, S′, and D′ would be expected to relate to each other for a given object is illustrated by Figure 2 and stated by the following equation (McCready, 1965, 1985, Ono, 1970, Komoda and Ono, 1974, Reed, 1989, Kaneko & Uchikawa, 1997).

Ross & Plug (2002, Page 31) dubbed this new rule the "perceptual size–distance invariance hypothesis".

Retinal size, "cortical size" and θ′

As already noted, the magnitude of an object's visual angle θ determines the size R of its retinal image. And, the size of the retinal image normally determines the extent of the neural activity pattern the retina's neural activity eventually generates in the primary visual cortex, area V1 or Brodmann area 17. This cortical area harbors a distorted but spatially isomorphic "map" of the retina (see Retinotopy). This neurological relationship recently was confirmed by Murray, Boyaci, & Kersten (2006) using functional magnetic resonance imaging.

The retinal image is not perceived or sensed. That is, experimental psychologists long ago rejected any idea that people "sense" a proximal stimulus such as the retinal image. As Gogel (1969, 1997) has repeatedly emphasized, there is no "sensation" which could be called the "perceived retinal image size", R′.

Also rejected is a popular idea that an object's "perceived size" results from a "scaling of retinal size"; an illogical process that somehow "magnifies" the very small "retinal size" to yield the viewed object's much larger perceived linear size S′.

Instead, the physical retinal extent R normally determines the magnitude of the perceived visual angle θ′. But, as already noted, "other factors" can intervene to slightly change θ′ for a target forming a constant sized retinal image (and thereby create a visual angle illusion). Indeed, the major discovery by Murray et al. (2006) concerns this flexible relationship between R and θ′, as described below.

Visual angle illusions and area V1

The Murray, et al. (2006) observers viewed a flat picture with two disks that subtended the same visual angle θ and formed retinal images of the same size (R), but the perceived angular size, θ′, for one disk was larger than θ′ for the other (say, 17% larger) due to differences in their background patterns. And, in cortical Area V1, the sizes of the activity patterns related to the disks were unequal, despite the fact that the retinal images were the same size. The difference between these "cortical sizes" in Area V1 for the illusion disks was essentially the same as the difference produced by two non-illusory disks whose retinal image sizes differed by, say, 17%.

The researchers pointed out that their findings dramatically disagree with the hypothetical models of neural events being proposed in nearly all current theories of visual spatial perception.

Murray, et al. (2006) also noted that the flat illusion pattern they used can represent other classic "size" illusions, such as the Ponzo illusion and, as well, the moon illusion which is a visual angle illusion for most observers, (McCready, 1965, 1986, Restle 1970, Plug & Ross, 1989, p. 21, Ross & Plug, 2002).

A detailed meta-analysis of the Murray et al. (2006) results is available in McCready (2007, Appendix B).

The size–distance paradox

The classical size–distance invariance hypothesis

Conventional "textbook" theories of "size" and distance perception do not refer to the perceived visual angle (e.g., Gregory, 1963, 1970, 1998, 2008) and some researchers even deny that it exists (Kaufman & Kaufman, 2002). This idea that one does not see the different directions in which objects lie from oneself is a basis of the so-called "size–distance invariance hypothesis" (SDIH).

That old SDIH logic (geometry) is typically illustrated using a diagram that resembles Figure 2, but has the physical visual angle θ substituted for the perceived visual angle θ′. The equation for the SDIH thus is

Here, S′ is typically called the "perceived size" or "apparent size"; more precisely it is the perceived linear size, measured in meters.

When rearranged as S′ = D′ tan θ, the equation expresses Emmert's law.

However, at least since 1962, researchers have pointed out that many classic "size" and distance illusions can be neither described nor explained using the SDIH, so a new hypothesis is needed (Boring 1962, Gruber, 1956, McCready, 1965, Baird, 1970, Ono 1970). For instance, consider the simple Ebbinghaus illusion.

Example: the Ebbinghaus illusion

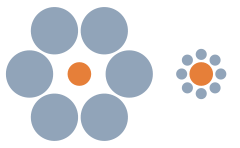
The two central circles are the same linear size S and the same viewing distance D, so they subtend the same visual angle θ and form equal-sized retinal images. But the lower one "looks larger" than the upper one.

According to the SDIH, "looks larger" can mean only that S′ is greater, and with the physical angle θ the same for both, the SDIH requires that D′ be greater for the lower one than for the upper one. However, for most observers, both circles appear unequal while also appearing at the same distance (on the same page).

This commonly found disagreement between published data and the SDIH is known as the "size–distance paradox" (Gruber, 1956, Ono, et al. 1974).

The "paradox" completely vanishes, however, when the illusion is described, instead, as basically a visual angle illusion: That is, the perceived visual angle θ′ is larger for the lower circle than for the upper circle: It is as if its retinal image were larger. So. according to the "new" perceptual invariance hypothesis, (S′ / D′ = tan θ′), with θ′ larger for the lower circle, and with D′ correctly the same for both circles, then S′ becomes larger for the lower one by the same ratio that θ′ is larger. That is, the reason the lower one looks a larger linear size on the page is because it looks a larger angular size than the upper one.

Explaining visual angle illusions remains difficult

The new hypothesis that includes θ′ along with S′ describes the Ebbinghaus illusion and many other classic "size" illusions more completely and more logically than does the popular SDIH. What still needs to be explained, however, is why the basic visual angle illusion occurs in each example.

Describing the few existing explanations for visual angle illusions is beyond the scope of this present entry. The most recent theories have been presented mostly in articles concerning the moon illusion (Baird et al., 1990, Enright, 1989a, 1989b, Hershenson, 1982, 1989b, Higashiyama, 1992, McCready 1986, 1999–2007, Plug & Ross, 1989, Reed, 1989, Roscoe, 1989, and especially in two "moon illusion" books (Hershenson, 1989; Ross & Plug, 2002) which make it quite clear that vision scientists have not yet agreed upon any particular theory of visual angle illusions.

There also is the lesser-known, but evidently the largest visual angle illusion of oculomotor micropsia (convergence micropsia) for which a few different explanations are being considered (McCready, 1965, 2007, Ono, 1970, Komoda & Ono, 1974, Ono, et al. 1974, Enright, 1987b, 1989a, 1989b).

This is a partial list of "size and distance" illusions that begin as visual angle illusions (angular size illusions) for most observers.

• Moon illusion
• Oculomotor micropsia (convergence micropsia)
• Ebbinghaus illusion (Titchner circles)
• Hering illusion
• Ponzo illusion
• Müller-Lyer illusion
• Orbison illusion
• Jastrow illusion
• Wundt illusion
• Curvature of the apparent fronto-parallel plane (AFPP)

Notes

References