Unambiguous finite automaton
In automata theory, an unambiguous finite automaton (UFA) is a special kind of a nondeterministic finite automaton (NFA). Each deterministic finite automaton (DFA) is an UFA, but not vice versa. DFA, UFA, and NFA recognize exactly the same class of formal languages. On the one hand, an NFA can be exponentially smaller than an equivalent DFA. On the other hand, some problems are easily solved on DFAs and not on UFAs. For example, given an automaton A, an automaton A' which accepts the complement of A can be computed in linear time when A is a DFA, it is not known whether it can be done in polynomial time for UFA. Hence UFAs are a mix of the worlds of DFA and of NFA; in some cases, they lead to smaller automata than DFA and quicker algorithms than NFA.
Formal definition
An NFA is represented formally by a 5-tuple, A=(Q, Σ, Δ, q0, F). An UFA is an NFA such that, for each word w = a1a2 … an, there exists at most one sequence of states r0,r1, …, rn, in Q with the following conditions:
- r0 = q0
- ri+1 ∈ Δ(ri, ai+1), for i = 0, …, n−1
- rn ∈ F.
In words, those conditions state that, if w is accepted by A, there is exactly one accepting path, that is, one path from an initial state to a final state, labelled by w.
Example
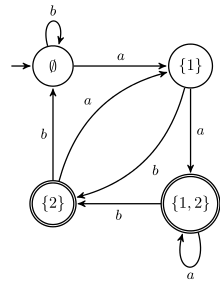
Let L be the set of words over the alphabet {a,b} whose nth last letter is an a. The figures show a DFA and a UFA accepting this language for n=2.
*a(a%2Bb)%5E2.svg.png)
The minimal DFA accepting L has 2n states, one for each subset of {1...n}. There is an UFA of n+1 states which accepts L: it guesses the nth last letter, and then verifies that only n-1 letters remain. It is indeed unambiguous as there exists only one nth last letter.
Inclusion and related problems
Three PSPACE-hard problems for general NFA belong to PTIME for DFA and are now considered.
Inclusion
It is decidable in polynomial-time whether an automaton's language is a subset of an automaton of another language.
| Sketch of the proof of inclusion |
|---|
|
Let A and B be two automata. Let L(A) and L(B) be the languages accepted by those automata. Then L(A)⊆L(B) if and only if L(A∩ B)=L(A), where A∩B denotes the Cartesian product automaton, which can be proven to be also unambiguous. Now, L(A∩B) is a subset of L(A) by construction; hence both set are equal if and only if for each length n∈ℕ, the number of words of length n in L(A∩B) is equal to the number of words of length n in L(A). It can be proved that is sufficient to check each n up to the product of the number of states of A and B. The number of words of length n accepted by an automaton can be computed in polynomial time using dynamic programming, which ends the proof.[1] |
Related problems
The problem of universality[note 1] and of equivalence, [note 2] also belong to PTIME, by reduction to the inclusion problem.
Checking whether an automaton in unambiguous
For a nondeterministic finite automaton A with n states and an m letter alphabet, it is decidable in time O(n2m) whether A is unambiguous.
| Sketch of the proof of unambiguity |
|---|
|
It suffices to use a fixpoint algorithm to compute the set of pairs of states q and q' such that there exists a word w which leads both to q and to q' . The automaton is unambiguous if and only if there is no such a pair such that both states are accepting. There are at most O(n2) state pairs, and for each pair there are m letters to consider to resume the fixpoint algorithm, hence the computation time. |
Some properties
- The cartesian product of two UFAs is a UFA.[2]
- The notion of unambiguity extends to finite state transducers and weighted automata. If a finite state transducer T is unambiguous, then each input word is associated by T to at most one output word. If a weighted automaton A is unambiguous, then the set of weight does not need to be a semiring, instead it suffices to consider a monoid. Indeed, there is at most one accepting path.
References
- Christof Lödig, Unambiguous Finite Automata, Developments in Language Theory, (2013) pp. 29–30 (Slides)