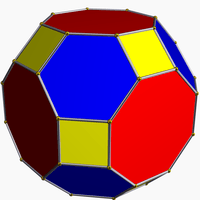
Truncated tetrahedron
| Truncated tetrahedron | |
|---|---|
 (Click here for rotating model) | |
| Type | Archimedean solid Uniform polyhedron |
| Elements | F = 8, E = 18, V = 12 (χ = 2) |
| Faces by sides | 4{3}+4{6} |
| Conway notation | tT |
| Schläfli symbols | t{3,3} = h2{4,3} |
| t0,1{3,3} | |
| Wythoff symbol | 2 3 | 3 |
| Coxeter diagram | |
| Symmetry group | Td, A3, [3,3], (*332), order 24 |
| Rotation group | T, [3,3]+, (332), order 12 |
| Dihedral Angle | 3-6: 109°28′16′ 6-6: 70°31′44″ |
| References | U02, C16, W6 |
| Properties | Semiregular convex |
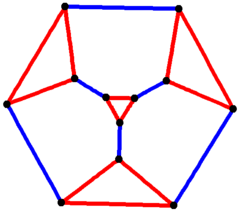
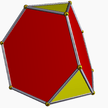 Colored faces |
 3.6.6 (Vertex figure) |
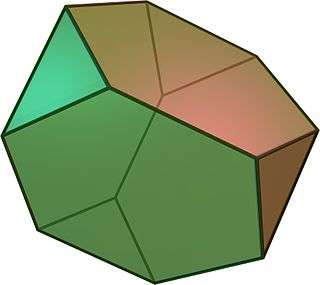
 Triakis tetrahedron (dual polyhedron) |
 Net |
In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 equilateral triangle faces, 12 vertices and 18 edges (of two types). It can be constructed by truncating all 4 vertices of a regular tetrahedron at one third of the original edge length.
A deeper truncation, removing a tetrahedron of half the original edge length from each vertex, is called rectification. The rectification of a tetrahedron produces an octahedron.[1]
A truncated tetrahedron is the Goldberg polyhedron GIII(1,1), containing triangular and hexagonal faces.
A truncated tetrahedron can be called a cantic cube, with Coxeter diagram, ![]()
![]()
![]()
![]()
![]() , having half of the vertices of the cantellated cube (rhombicuboctahedron),
, having half of the vertices of the cantellated cube (rhombicuboctahedron), ![]()
![]()
![]()
![]()
![]() . There are two dual positions of this construction, and combining them creates the uniform compound of two truncated tetrahedra.
. There are two dual positions of this construction, and combining them creates the uniform compound of two truncated tetrahedra.
Area and volume
The area A and the volume V of a truncated tetrahedron of edge length a are:
Densest Packing
The densest packing of the Archimedean truncated tetrahedron is believed to be Φ = 207/208, as reported by two independent groups using Monte Carlo methods.[2][3] Although no mathematical proof exists that this is the best possible packing for the truncated tetrahedron, the high proximity to the unity and independency of the findings make it unlikely that an even denser packing is to be found. In fact, if the truncation of the corners is slightly smaller than that of an Archimedean truncated tetrahedron, this new shape can be used to completely fill space.[2]
Cartesian coordinates
Cartesian coordinates for the 12 vertices of a truncated tetrahedron centered at the origin, with edge length √8, are all permutations of (±1,±1,±3) with an even number of minus signs:
- (+3,+1,+1), (+1,+3,+1), (+1,+1,+3)
- (−3,−1,+1), (−1,−3,+1), (−1,−1,+3)
- (−3,+1,−1), (−1,+3,−1), (−1,+1,−3)
- (+3,−1,−1), (+1,−3,−1), (+1,−1,−3)
 |
 |
 |
| Orthogonal projection showing Cartesian coordinates inside it bounding box: (±3,±3,±3). | The hexagonal faces of the truncated tetrahedra can be divided into 6 coplanar equilateral triangles. The 4 new vertices have Cartesian coordinates: (−1,−1,−1), (−1,+1,+1), (+1,−1,+1), (+1,+1,−1). |
The set of vertex permutations (±1,±1,±3) with an odd number of minus signs forms a complementary truncated tetrahedron, and combined they form a uniform compound polyhedron. |
Another simple construction exists in 4-space as cells of the truncated 16-cell, with vertices as coordinate permutation of:
- (0,0,1,2)
Orthogonal projection
| Centered by | Edge normal | Face normal | Edge | Face/vertex |
|---|---|---|---|---|
| Image |  |
 |
 |
 |
| Dual image |  |
 |
 |
 |
| Projective symmetry |
[1] | [1] | [3] | [4] |
Spherical tiling
The truncated tetrahedron can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.
 |
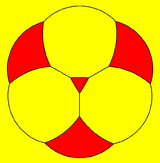 triangle-centered |
 hexagon-centered | |
| Orthographic projection | Stereographic projections | ||
|---|---|---|---|
Friauf polyhedron
A lower symmetry version of the truncated tetrahedron (a truncated tetragonal disphenoid with order 8 D2d symmetry) is called a Friauf polyhedron in crystals such as complex metallic alloys. This form fits 5 Friauf polyhedra around an axis, giving a 72-degree dihedral angle on a subset of 6-6 edges.[4] Its named after J. B. Friauf and his 1927 paper "The crystal structure of the intermetallic compound MgCu2".[5]
Use in architecture
Giant truncated tetrahedra were used for the "Man the Explorer" and "Man the Producer" theme pavilions in Expo 67. They were made of massive girders of steel bolted together in a geometric lattice. The truncated tetrahedra were interconnected with lattice steel platforms. All of these buildings were demolished after the end of Expo 67, as they had not been built to withstand the severity of the Montreal weather over the years. Their only remnants are in the Montreal city archives, the Public Archives Of Canada and the photo collections of tourists of the times.[6]
Truncated tetrahedral graph
| Truncated tetrahedral graph | |
|---|---|
|
3-fold symmetry | |
| Vertices | 12[7] |
| Edges | 18 |
| Radius | 3 |
| Diameter | 3[7] |
| Girth | 3[7] |
| Automorphisms | 24 (S4)[7] |
| Chromatic number | 3[7] |
| Chromatic index | 3[7] |
| Properties | Hamiltonian, regular, 3-vertex-connected, planar graph |
In the mathematical field of graph theory, a truncated tetrahedral graph is a Archimedean graph, the graph of vertices and edges of the truncated tetrahedron, one of the Archimedean solids. It has 12 vertices and 18 edges.[8] It is a connected cubic graph,[9] and connected cubic transitive graph.[10]
| Circular | Orthographic projections | |
|---|---|---|
 |
 4-fold symmetry |
 3-fold symmetry |
Related polyhedra and tilings
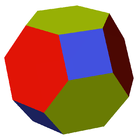
| Family of uniform tetrahedral polyhedra | |||||||
|---|---|---|---|---|---|---|---|
| Symmetry: [3,3], (*332) | [3,3]+, (332) | ||||||
 |
 |
 |
 |
 |
 |
 |
 |
| {3,3} | t{3,3} | r{3,3} | t{3,3} | {3,3} | rr{3,3} | tr{3,3} | sr{3,3} |
| Duals to uniform polyhedra | |||||||
 |
 |
 |
 |
 | |||
| V3.3.3 | V3.6.6 | V3.3.3.3 | V3.6.6 | V3.3.3 | V3.4.3.4 | V4.6.6 | V3.3.3.3.3 |
It is also a part of a sequence of cantic polyhedra and tilings with vertex configuration 3.6.n.6. In this wythoff construction the edges between the hexagons represent degenerate digons.
 |
Orbifold *n32 |
Spherical | Euclidean | Hyperbolic | Paracompact | ||
|---|---|---|---|---|---|---|---|
| *332 | *333 | *433 | *533 | *633... | *∞33 | ||
| Cantic figure |  |
 |
 |
 |
 |
 | |
| Vertex | 3.6.2.6 | 3.6.3.6 | 3.6.4.6 | 3.6.5.6 | 3.6.6.6 | 3.6.∞.6 | |
Symmetry mutations
This polyhedron is topologically related as a part of sequence of uniform truncated polyhedra with vertex configurations (3.2n.2n), and [n,3] Coxeter group symmetry.
| *n32 symmetry mutation of truncated spherical tilings: t{n,3} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paraco. | |||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] | ||||
| Truncated figures |
|
 |
 |
 |
 |
 |
 |
 | |||
| Symbol | t{2,3} | t{3,3} | t{4,3} | t{5,3} | t{6,3} | t{7,3} | t{8,3} | t{∞,3} | |||
| Triakis figures |
 |
 |
 |
 |
 |
 | |||||
| Config. | V3.4.4 | V3.6.6 | V3.8.8 | V3.10.10 | V3.12.12 | V3.14.14 | V3.16.16 | V3.∞.∞ | |||
See also
- Quarter cubic honeycomb – Fills space using truncated tetrahedra and smaller tetrahedra
- Truncated 5-cell – Similar uniform polytope in 4-dimensions
- Truncated triakis tetrahedron
- Triakis truncated tetrahedron
- Octahedron – a rectified tetrahedron
References
- ↑ Chisholm, Matt; Avnet, Jeremy (1997). "Truncated Trickery: Truncatering". theory.org. Retrieved 2013-09-02.
- 1 2 Damasceno, Pablo F.; Engel, Michael; Glotzer, Sharon C. (Dec 2011). "Crystalline Assemblies and Densest Packings of a Family of Truncated Tetrahedra and the Role of Directional Entropic Forces". ACS Nano. 6 (2012): 609–614. arXiv:1109.1323
 . doi:10.1021/nn204012y.
. doi:10.1021/nn204012y. - ↑ Jiao, Yang; Torquato, Sal (Sep 2011). "A Packing of Truncated Tetrahedra that Nearly Fills All of Space". arXiv:1107.2300
 [cond-mat.soft].
[cond-mat.soft]. - ↑ http://met.iisc.ernet.in/~lord/webfiles/clusters/polyclusters.pdf
- ↑ Friauf, J. B. (1927). "The crystal structure of the intermetallic compound MgCu2". J. Am. Chem. Soc. 19: 3107–3114.
- ↑ http://expo67.ncf.ca/man_the_producer_p1.html
- 1 2 3 4 5 6 An Atlas of Graphs, page=172, C105
- ↑ An Atlas of Graphs, page 267, truncated tetrahedral graph
- ↑ An Atlas of Graphs, page 130, connected cubic graphs, 12 vertices, C105
- ↑ An Atlas of Graphs, page 161, connected cubic transitive graphs, 12 vertices, Ct11
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
- Read, R. C.; Wilson, R. J. (1998), An Atlas of Graphs, Oxford University Press
External links
- Klitzing, Richard. "3D convex uniform polyhedra x3x3o - tut".
- Editable printable net of a truncated tetrahedron with interactive 3D view
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra