Trigonometric number
In mathematics, a trigonometric number[1]:ch. 5 is an irrational number produced by taking the sine or cosine of a rational multiple of a circle, or equivalently, the sine or cosine of an angle which in radians is a rational multiple of π, or the sine or cosine of a rational number of degrees.
A real number different of 0, 1, –1 is a trigonometric number if and only if it is the real part of a root of unity.
Ivan Niven gave proofs of theorems regarding these numbers.[1][2]:ch. 3 Li Zhou and Lubomir Markov[3] recently improved and simplified Niven's proofs.
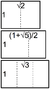
Any trigonometric number can be expressed in terms of radicals.[4] For example,
Thus every trigonometric number is an algebraic number. This latter statement can be proved[2]:pp. 29-30 by starting with the statement of de Moivre's formula for the case of for coprime k and n:
Expanding the left side and equating real parts gives an equation in and substituting gives a polynomial equation having as a solution, so by definition the latter is an algebraic number. Also is algebraic since it equals the algebraic number Finally, where again is a rational multiple of is algebraic as can be seen by equating the imaginary parts of the expansion of the de Moivre equation and dividing through by to obtain a polynomial equation in
See also
References
- 1 2 Niven, Ivan. Numbers: Rational and Irrational, 1961.
- 1 2 Niven, Ivan. Irrational Numbers, Carus Mathematical Monographs no. 11, 1956.
- ↑ Li Zhou and Lubomir Markov (2010). "Recurrent Proofs of the Irrationality of Certain Trigonometric Values". American Mathematical Monthly. 117 (4): 360–362. doi:10.4169/000298910x480838. http://arxiv.org/abs/0911.1933
- ↑ Weisstein, Eric W. "Trigonometry Angles." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/TrigonometryAngles.html