Traced monoidal category

In category theory, a traced monoidal category is a category with some extra structure which gives a reasonable notion of feedback.

A traced symmetric monoidal category is a symmetric monoidal category C together with a family of functions

\mathrm {Tr} _{X,Y}^{U}:\mathbf {C} (X\otimes U,Y\otimes U)\to \mathbf {C} (X,Y)

called a trace, satisfying the following conditions (where we sometimes denote an identity morphism by the corresponding object, e.g., using U to denote ${\text{id}}_{U}$ ):

naturality in X: for every $f:X\otimes U\to Y\otimes U$ and $g:X'\to X$ ,

\mathrm {Tr} _{X,Y}^{U}(f)g=\mathrm {Tr} _{X',Y}^{U}(f(g\otimes U))

Naturality in X

naturality in Y: for every $f:X\otimes U\to Y\otimes U$ and $g:Y\to Y'$ ,

g\mathrm {Tr} _{X,Y}^{U}(f)=\mathrm {Tr} _{X,Y'}^{U}((g\otimes U)f)

Naturality in Y

dinaturality in U: for every $f:X\otimes U\to Y\otimes U'$ and $g:U'\to U$

\mathrm {Tr} _{X,Y}^{U}((Y\otimes g)f)=\mathrm {Tr} _{X,Y}^{U'}(f(X\otimes g))

Dinaturality in U

vanishing I: for every $f:X\otimes I\to Y\otimes I$ ,

\mathrm {Tr} _{X,Y}^{I}(f)=f

Vanishing I

vanishing II: for every $f:X\otimes U\otimes V\to Y\otimes U\otimes V$

\mathrm {Tr} _{X,Y}^{U\otimes V}(f)=\mathrm {Tr} _{X,Y}^{U}(\mathrm {Tr} _{X\otimes U,Y\otimes U}^{V}(f))

Vanishing II

superposing: for every $f:X\otimes U\to Y\otimes U$ and $g:W\to Z$ ,

g\otimes \mathrm {Tr} _{X,Y}^{U}(f)=\mathrm {Tr} _{W\otimes X,Z\otimes Y}^{U}(g\otimes f)

Superposing

yanking:

\mathrm {Tr} _{X,X}^{X}(\gamma _{X,X})=X

(where $\gamma$ is the symmetry of the monoidal category).

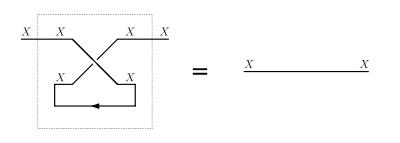
Yanking

Properties

Every compact closed category admits a trace.
Given a traced monoidal category C, the Int construction generates the free (in some bicategorical sense) compact closure Int(C) of C.

References

André Joyal, Ross Street, Dominic Verity (1996). "Traced monoidal categories". Mathematical Proceedings of the Cambridge Philosophical Society. 3: 447–468. doi:10.1017/S0305004100074338.

This article is issued from Wikipedia - version of the 3/23/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.