Terrace ledge kink model

In chemistry, the Terrace Ledge Kink model (TLK), which is also referred to as the Terrace Step Kink model (TSK), describes the thermodynamics of crystal surface formation and transformation, as well as the energetics of surface defect formation. It is based upon the idea that the energy of an atom’s position on a crystal surface is determined by its bonding to neighboring atoms and that transitions simply involve the counting of broken and formed bonds. The TLK model can be applied to surface science topics such as crystal growth, surface diffusion, roughening, and vaporization.

History

The TLK model is credited as having originated from papers published in the 1920s by two German chemists W. Kossel^[1] and I. N. Stranski^[2] wherein the thermodynamic stability of step edges were discussed.

Definitions

Figure 1: The names for the various atomic positions in the TLK model. This graphic representation is for a simple cubic lattice.

Figure 2: A scanning tunneling microscope image of a clean silicon (100) surface showing a step edge as well as many surface vacancies. Many kink sites are visible along the terrace edge. The rows visible are dimer rows in a 2x1 reconstruction.

Depending on the position of an atom on a surface, it can be referred to by one of several names. Figure 1 illustrates the names for the atomic positions and point defects on a surface for a simple cubic lattice.

Figure 2 shows a scanning tunneling microscopy topographic image of a step edge that shows many of the features in Figure 1.

Thermodynamics

The energy required to remove an atom from the surface depends on the number of bonds to other surface atoms which must be broken. For a simple cubic lattice in this model, each atom is treated as a cube and bonding occurs at each face, giving a coordination number of 6 nearest neighbors. Second-nearest neighbors in this cubic model are those that share an edge and third-nearest neighbors are those that share corners. The number of neighbors, second-nearest neighbors, and third-nearest neighbors for each of the different atom positions are given in Table 1.^[3]

Table 1: Number of neighbors for various atomic positions for a simple cubic lattice
Atom	Nearest Neighbors	Second-Nearest Neighbors	Third-Nearest Neighbors
Adatom	1	4	4
Step adatom	2	6	4
Kink atom	3	6	4
Step atom	4	6	4
Surface atom	5	8	4
Bulk atom	6	12	8

Most crystals, however, are not arranged in a simple cubic lattice. The same ideas apply for other types of lattices where the coordination number is not six, but these are not as easy to visualize and work with in theory, so the remainder of the discussion will focus on simple cubic lattices. Table 2 indicates the number of neighboring atoms for a bulk atom in some other crystal lattices.^[3]

Table 2: Number of neighboring atoms for a bulk atom for some crystal lattices
Lattice	Nearest Neighbors	Second-Nearest Neighbors	Third-Nearest Neighbors
Simple cubic	6	12	8
Face-centered cubic	12	6	24
Body-centered cubic	8	6	12
Hexagonal close packed	12	6	2
Diamond	4	12	12

The kink site is of special importance when evaluating the thermodynamics of a variety of phenomena. This site is also referred to as the “half-crystal position” and energies are evaluated relative to this position for processes such as adsorption, surface diffusion, and sublimation.^[4] The term “half-crystal” comes from the fact that the kink site has half the number of neighboring atoms as an atom in the crystal bulk, regardless of the type of crystal lattice.

For example, the formation energy for an adatom—ignoring any crystal relaxation—is calculated by subtracting the energy of an adatom from the energy of the kink atom.

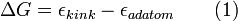\Delta G = \epsilon_{kink} - \epsilon_{adatom} \qquad (1)

This can be understood as the breaking of all of the kink atom’s bonds to remove the atom from the surface and then reforming the adatom interactions. This is equivalent to a kink atom diffusing away from the rest of the step to become a step adatom and then diffusing away from the adjacent step onto the terrace to become an adatom. In the case where all interactions are ignored except for those with nearest neighbors, the formation energy for an adatom would be the following, where 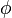$\phi$ is the bond energy in the crystal is given by Equation 2.

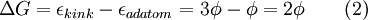\Delta G = \epsilon_{kink} - \epsilon_{adatom} = 3\phi - \phi = 2\phi \qquad (2)

This can be extended to a variety of situations, such as the formation of an adatom-surface vacancy pair on a terrace, which would involve the removal of a surface atom from the crystal and placing it as an adatom on the terrace. This is described by Equation 3.

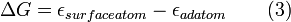\Delta G = \epsilon_{surface atom} - \epsilon_{adatom} \qquad (3)

^[3]

The energy of sublimation would simply be the energy required to remove an atom from the kink site. This can be envisioned as the surface being disassembled one terrace at a time by removing atoms from the edge of each step, which is the kink position. It has been demonstrated that the application of an external electric field will induce the formation of additional kinks in a surface, which then leads to a faster rate of evaporation from the surface.^[5]

Temperature dependence of defect coverage

The number of adatoms present on a surface is temperature dependent. The relationship between the surface adatom concentration and the temperature at equilibrium is described by equation 4, where n₀ is the total number of surface sites per unit area:

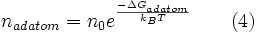n_{adatom}=n_0 e^\frac{-\Delta G_{adatom}}{k_BT} \qquad (4)

^[3]

This can be extended to find the equilibrium concentration of other types of surface point defects as well. To do so, the energy of the defect in question is simply substituted into the above equation in the place of the energy of adatom formation.

References

↑ Kossel, W., Extenoling the Law of Bravais [M]. Nach Ges Wiss Gottingen 1927, 143.
↑ Stranski, I. N., Zur Theorie des Kristallwachstums. Z. Phys. Chem 1928, 136, 259-278.
1 2 3 4 Oura, K.; Lifshits, V. G.; Saranin, A. A.; Zotov, A. V.; Katayama, M.; Yates, J. T., Surface Science: An Introduction. Springer-Verlag: Berlin, 2003.
↑ Imai, Y.; Mukaida, M.; Watanabe, A.; Tsunoda, T., Formation energies of two-dimensional nuclei randomly-generated on (001), (110), and (111) planes of a face-centered-cubic crystal. Thin Solid Films 1997, 300, (1-2), 305-313.
↑ Munir, Z., Ledgewlse vaporization. Metallurgical and Materials Transactions A 1991, 22, (6), 1305-1310.

This article is issued from Wikipedia - version of the 10/23/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.