Table of congruences

In mathematics, a congruence is an equivalence relation on the integers. The following table lists important or interesting congruences.

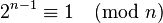$2^{n-1} \equiv 1 \pmod{n}\,\!$	special case of Fermat's little theorem, satisfied by all odd prime numbers
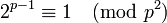$2^{p-1} \equiv 1 \pmod{p^2}\,\!$	solutions are called Wieferich primes
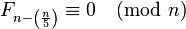$F_{n - \left(\frac{{n}}{{5}}\right)} \equiv 0 \pmod{n}$	satisfied by all prime numbers
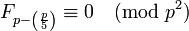$F_{p - \left(\frac{{p}}{{5}}\right)} \equiv 0 \pmod{p^2}$	solutions are called Wall–Sun–Sun primes
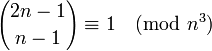${2n-1 \choose n-1} \equiv 1 \pmod{n^3}$	by Wolstenholme's theorem satisfied by all prime numbers greater than 3
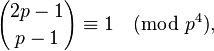${2p-1 \choose p-1} \equiv 1 \pmod{p^4},$	solutions are called Wolstenholme primes
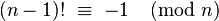$(n-1)!\ \equiv\ -1 \pmod n$	by Wilson's theorem a natural number n is prime if and only if it satisfies this congruence
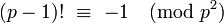$(p-1)!\ \equiv\ -1 \pmod{p^2}$	solutions are called Wilson primes

References

This article is issued from Wikipedia - version of the 7/21/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.