Standard normal table
A standard normal table, also called the unit normal table or Z table, is a mathematical table for the values of Φ, which are the values of the cumulative distribution function of the normal distribution. It is used to find the probability that a statistic is observed below, above, or between values on the standard normal distribution, and by extension, any normal distribution. Since probability tables cannot be printed for every normal distribution, as there are an infinite variety of normal distributions, it is common practice to convert a normal to a standard normal and then use the standard normal table to find probabilities.[1]
Normal and standard normal distribution
Normal distributions are symmetrical, bell-shaped distributions that are useful in describing real-world data. The standard normal distribution, represented by the letter Z, is the normal distribution having a mean of 0 and a standard deviation of 1.
Conversion
If X is a random variable from a normal distribution with mean μ and standard deviation σ, its Z-score may be calculated from X by subtracting μ and dividing by σ.
For the average of a sample from a population n in which the mean is μ and the standard deviation is S, the standard error is S/√n:
Reading a Z table
Formatting / layout
Z tables are typically composed as follows:
- The label for rows contains the integer part and the first decimal place of Z.
- The label for columns contains the second decimal place of Z.
- The values within the table are the probabilities corresponding to the table type. These probabilities are calculations of the area under the normal curve from the starting point (0 for cumulative from mean, negative infinity for cumulative and positive infinity for complementary cumulative) to Z.
Example: To find 0.69, one would look down the rows to find 0.6 and then across the columns to 0.09 which would yield a probability of 0.25490 for a cumulative from mean table or 0.75490 from a cumulative table.
Because the normal distribution curve is symmetrical, probabilities for only positive values of Z are typically given. The user has to use a complementary operation on the absolute value of Z, as in the example below.
Types of tables
Z tables use at least three different conventions:
- Cumulative from mean
- gives a probability that a statistic is between 0 (mean) and Z. Example: Prob(0 ≤ Z ≤ 0.69) = 0.2549
- Cumulative
- gives a probability that a statistic is less than Z. This equates to the area of the distribution below Z. Example: Prob(Z ≤ 0.69) = 0.7549.
- Complementary cumulative
- gives a probability that a statistic is greater than Z. This equates to the area of the distribution above Z.
- Example: Find Prob(Z ≥ 0.69). Since this is the portion of the area above Z, the proportion that is greater than Z is found by subtracting Z from 1. That is Prob(Z ≥ 0.69) = 1 - Prob(Z ≤ 0.69) or Prob(Z ≥ 0.69) = 1 - 0.7549 = 0.2451.
Table examples
Cumulative from mean (0 to Z)
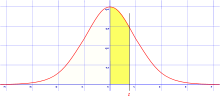
This table gives a probability that a statistic is between 0 (the mean) and Z.
| z | +0.00 | +0.01 | +0.02 | +0.03 | +0.04 | +0.05 | +0.06 | +0.07 | +0.08 | +0.09 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.00000 | 0.00399 | 0.00798 | 0.01197 | 0.01595 | 0.01994 | 0.02392 | 0.02790 | 0.03188 | 0.03586 | |
| 0.1 | 0.03980 | 0.04380 | 0.04776 | 0.05172 | 0.05567 | 0.05966 | 0.06360 | 0.06749 | 0.07142 | 0.07535 | |
| 0.2 | 0.07930 | 0.08317 | 0.08706 | 0.09095 | 0.09483 | 0.09871 | 0.10257 | 0.10642 | 0.11026 | 0.11409 | |
| 0.3 | 0.11791 | 0.12172 | 0.12552 | 0.12930 | 0.13307 | 0.13683 | 0.14058 | 0.14431 | 0.14803 | 0.15173 | |
| 0.4 | 0.15542 | 0.15910 | 0.16276 | 0.16640 | 0.17003 | 0.17364 | 0.17724 | 0.18082 | 0.18439 | 0.18793 | |
| 0.5 | 0.19146 | 0.19497 | 0.19847 | 0.20194 | 0.20540 | 0.20884 | 0.21226 | 0.21566 | 0.21904 | 0.22240 | |
| 0.6 | 0.22575 | 0.22907 | 0.23237 | 0.23565 | 0.23891 | 0.24215 | 0.24537 | 0.24857 | 0.25175 | 0.25490 | |
| 0.7 | 0.25804 | 0.26115 | 0.26424 | 0.26730 | 0.27035 | 0.27337 | 0.27637 | 0.27935 | 0.28230 | 0.28524 | |
| 0.8 | 0.28814 | 0.29103 | 0.29389 | 0.29673 | 0.29955 | 0.30234 | 0.30511 | 0.30785 | 0.31057 | 0.31327 | |
| 0.9 | 0.31594 | 0.31859 | 0.32121 | 0.32381 | 0.32639 | 0.32894 | 0.33147 | 0.33398 | 0.33646 | 0.33891 | |
| 1.0 | 0.34134 | 0.34375 | 0.34614 | 0.34849 | 0.35083 | 0.35314 | 0.35543 | 0.35769 | 0.35993 | 0.36214 | |
| 1.1 | 0.36433 | 0.36650 | 0.36864 | 0.37076 | 0.37286 | 0.37493 | 0.37698 | 0.37900 | 0.38100 | 0.38298 | |
| 1.2 | 0.38493 | 0.38686 | 0.38877 | 0.39065 | 0.39251 | 0.39435 | 0.39617 | 0.39796 | 0.39973 | 0.40147 | |
| 1.3 | 0.40320 | 0.40490 | 0.40658 | 0.40824 | 0.40988 | 0.41149 | 0.41308 | 0.41466 | 0.41621 | 0.41774 | |
| 1.4 | 0.41924 | 0.42073 | 0.42220 | 0.42364 | 0.42507 | 0.42647 | 0.42785 | 0.42922 | 0.43056 | 0.43189 | |
| 1.5 | 0.43319 | 0.43448 | 0.43574 | 0.43699 | 0.43822 | 0.43943 | 0.44062 | 0.44179 | 0.44295 | 0.44408 | |
| 1.6 | 0.44520 | 0.44630 | 0.44738 | 0.44845 | 0.44950 | 0.45053 | 0.45154 | 0.45254 | 0.45352 | 0.45449 | |
| 1.7 | 0.45543 | 0.45637 | 0.45728 | 0.45818 | 0.45907 | 0.45994 | 0.46080 | 0.46164 | 0.46246 | 0.46327 | |
| 1.8 | 0.46407 | 0.46485 | 0.46562 | 0.46638 | 0.46712 | 0.46784 | 0.46856 | 0.46926 | 0.46995 | 0.47062 | |
| 1.9 | 0.47128 | 0.47193 | 0.47257 | 0.47320 | 0.47381 | 0.47441 | 0.47500 | 0.47558 | 0.47615 | 0.47670 | |
| 2.0 | 0.47725 | 0.47778 | 0.47831 | 0.47882 | 0.47932 | 0.47982 | 0.48030 | 0.48077 | 0.48124 | 0.48169 | |
| 2.1 | 0.48214 | 0.48257 | 0.48300 | 0.48341 | 0.48382 | 0.48422 | 0.48461 | 0.48500 | 0.48537 | 0.48574 | |
| 2.2 | 0.48610 | 0.48645 | 0.48679 | 0.48713 | 0.48745 | 0.48778 | 0.48809 | 0.48840 | 0.48870 | 0.48899 | |
| 2.3 | 0.48928 | 0.48956 | 0.48983 | 0.49010 | 0.49036 | 0.49061 | 0.49086 | 0.49111 | 0.49134 | 0.49158 | |
| 2.4 | 0.49180 | 0.49202 | 0.49224 | 0.49245 | 0.49266 | 0.49286 | 0.49305 | 0.49324 | 0.49343 | 0.49361 | |
| 2.5 | 0.49379 | 0.49396 | 0.49413 | 0.49430 | 0.49446 | 0.49461 | 0.49477 | 0.49492 | 0.49506 | 0.49520 | |
| 2.6 | 0.49534 | 0.49547 | 0.49560 | 0.49573 | 0.49585 | 0.49598 | 0.49609 | 0.49621 | 0.49632 | 0.49643 | |
| 2.7 | 0.49653 | 0.49664 | 0.49674 | 0.49683 | 0.49693 | 0.49702 | 0.49711 | 0.49720 | 0.49728 | 0.49736 | |
| 2.8 | 0.49744 | 0.49752 | 0.49760 | 0.49767 | 0.49774 | 0.49781 | 0.49788 | 0.49795 | 0.49801 | 0.49807 | |
| 2.9 | 0.49813 | 0.49819 | 0.49825 | 0.49831 | 0.49836 | 0.49841 | 0.49846 | 0.49851 | 0.49856 | 0.49861 | |
| 3.0 | 0.49865 | 0.49869 | 0.49874 | 0.49878 | 0.49882 | 0.49886 | 0.49889 | 0.49893 | 0.49896 | 0.49900 | |
Cumulative
This table gives a probability that a statistic is less than Z (i.e. between negative infinity and Z).
| z | +0.00 | +0.01 | +0.02 | +0.03 | +0.04 | +0.05 | +0.06 | +0.07 | +0.08 | +0.09 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.50000 | 0.50399 | 0.50798 | 0.51197 | 0.51595 | 0.51994 | 0.52392 | 0.52790 | 0.53188 | 0.53586 | |
| 0.1 | 0.53980 | 0.54380 | 0.54776 | 0.55172 | 0.55567 | 0.55966 | 0.56360 | 0.56749 | 0.57142 | 0.57535 | |
| 0.2 | 0.57930 | 0.58317 | 0.58706 | 0.59095 | 0.59483 | 0.59871 | 0.60257 | 0.60642 | 0.61026 | 0.61409 | |
| 0.3 | 0.61791 | 0.62172 | 0.62552 | 0.62930 | 0.63307 | 0.63683 | 0.64058 | 0.64431 | 0.64803 | 0.65173 | |
| 0.4 | 0.65542 | 0.65910 | 0.66276 | 0.66640 | 0.67003 | 0.67364 | 0.67724 | 0.68082 | 0.68439 | 0.68793 | |
| 0.5 | 0.69146 | 0.69497 | 0.69847 | 0.70194 | 0.70540 | 0.70884 | 0.71226 | 0.71566 | 0.71904 | 0.72240 | |
| 0.6 | 0.72575 | 0.72907 | 0.73237 | 0.73565 | 0.73891 | 0.74215 | 0.74537 | 0.74857 | 0.75175 | 0.75490 | |
| 0.7 | 0.75804 | 0.76115 | 0.76424 | 0.76730 | 0.77035 | 0.77337 | 0.77637 | 0.77935 | 0.78230 | 0.78524 | |
| 0.8 | 0.78814 | 0.79103 | 0.79389 | 0.79673 | 0.79955 | 0.80234 | 0.80511 | 0.80785 | 0.81057 | 0.81327 | |
| 0.9 | 0.81594 | 0.81859 | 0.82121 | 0.82381 | 0.82639 | 0.82894 | 0.83147 | 0.83398 | 0.83646 | 0.83891 | |
| 1.0 | 0.84134 | 0.84375 | 0.84614 | 0.84849 | 0.85083 | 0.85314 | 0.85543 | 0.85769 | 0.85993 | 0.86214 | |
| 1.1 | 0.86433 | 0.86650 | 0.86864 | 0.87076 | 0.87286 | 0.87493 | 0.87698 | 0.87900 | 0.88100 | 0.88298 | |
| 1.2 | 0.88493 | 0.88686 | 0.88877 | 0.89065 | 0.89251 | 0.89435 | 0.89617 | 0.89796 | 0.89973 | 0.90147 | |
| 1.3 | 0.90320 | 0.90490 | 0.90658 | 0.90824 | 0.90988 | 0.91149 | 0.91308 | 0.91466 | 0.91621 | 0.91774 | |
| 1.4 | 0.91924 | 0.92073 | 0.92220 | 0.92364 | 0.92507 | 0.92647 | 0.92785 | 0.92922 | 0.93056 | 0.93189 | |
| 1.5 | 0.93319 | 0.93448 | 0.93574 | 0.93699 | 0.93822 | 0.93943 | 0.94062 | 0.94179 | 0.94295 | 0.94408 | |
| 1.6 | 0.94520 | 0.94630 | 0.94738 | 0.94845 | 0.94950 | 0.95053 | 0.95154 | 0.95254 | 0.95352 | 0.95449 | |
| 1.7 | 0.95543 | 0.95637 | 0.95728 | 0.95818 | 0.95907 | 0.95994 | 0.96080 | 0.96164 | 0.96246 | 0.96327 | |
| 1.8 | 0.96407 | 0.96485 | 0.96562 | 0.96638 | 0.96712 | 0.96784 | 0.96856 | 0.96926 | 0.96995 | 0.97062 | |
| 1.9 | 0.97128 | 0.97193 | 0.97257 | 0.97320 | 0.97381 | 0.97441 | 0.97500 | 0.97558 | 0.97615 | 0.97670 | |
| 2.0 | 0.97725 | 0.97778 | 0.97831 | 0.97882 | 0.97932 | 0.97982 | 0.98030 | 0.98077 | 0.98124 | 0.98169 | |
| 2.1 | 0.98214 | 0.98257 | 0.98300 | 0.98341 | 0.98382 | 0.98422 | 0.98461 | 0.98500 | 0.98537 | 0.98574 | |
| 2.2 | 0.98610 | 0.98645 | 0.98679 | 0.98713 | 0.98745 | 0.98778 | 0.98809 | 0.98840 | 0.98870 | 0.98899 | |
| 2.3 | 0.98928 | 0.98956 | 0.98983 | 0.99010 | 0.99036 | 0.99061 | 0.99086 | 0.99111 | 0.99134 | 0.99158 | |
| 2.4 | 0.99180 | 0.99202 | 0.99224 | 0.99245 | 0.99266 | 0.99286 | 0.99305 | 0.99324 | 0.99343 | 0.99361 | |
| 2.5 | 0.99379 | 0.99396 | 0.99413 | 0.99430 | 0.99446 | 0.99461 | 0.99477 | 0.99492 | 0.99506 | 0.99520 | |
| 2.6 | 0.99534 | 0.99547 | 0.99560 | 0.99573 | 0.99585 | 0.99598 | 0.99609 | 0.99621 | 0.99632 | 0.99643 | |
| 2.7 | 0.99653 | 0.99664 | 0.99674 | 0.99683 | 0.99693 | 0.99702 | 0.99711 | 0.99720 | 0.99728 | 0.99736 | |
| 2.8 | 0.99744 | 0.99752 | 0.99760 | 0.99767 | 0.99774 | 0.99781 | 0.99788 | 0.99795 | 0.99801 | 0.99807 | |
| 2.9 | 0.99813 | 0.99819 | 0.99825 | 0.99831 | 0.99836 | 0.99841 | 0.99846 | 0.99851 | 0.99856 | 0.99861 | |
| 3.0 | 0.99865 | 0.99869 | 0.99874 | 0.99878 | 0.99882 | 0.99886 | 0.99889 | 0.99893 | 0.99896 | 0.99900 | |
Complementary cumulative
This table gives a probability that a statistic is greater than Z.
| z | +0.00 | +0.01 | +0.02 | +0.03 | +0.04 | +0.05 | +0.06 | +0.07 | +0.08 | +0.09 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.50000 | 0.49601 | 0.49202 | 0.48803 | 0.48405 | 0.48006 | 0.47608 | 0.47210 | 0.46812 | 0.46414 | |
| 0.1 | 0.46020 | 0.45620 | 0.45224 | 0.44828 | 0.44433 | 0.44034 | 0.43640 | 0.43251 | 0.42858 | 0.42465 | |
| 0.2 | 0.42070 | 0.41683 | 0.41294 | 0.40905 | 0.40517 | 0.40129 | 0.39743 | 0.39358 | 0.38974 | 0.38591 | |
| 0.3 | 0.38209 | 0.37828 | 0.37448 | 0.37070 | 0.36693 | 0.36317 | 0.35942 | 0.35569 | 0.35197 | 0.34827 | |
| 0.4 | 0.34458 | 0.34090 | 0.33724 | 0.33360 | 0.32997 | 0.32636 | 0.32276 | 0.31918 | 0.31561 | 0.31207 | |
| 0.5 | 0.30854 | 0.30503 | 0.30153 | 0.29806 | 0.29460 | 0.29116 | 0.28774 | 0.28434 | 0.28096 | 0.27760 | |
| 0.6 | 0.27425 | 0.27093 | 0.26763 | 0.26435 | 0.26109 | 0.25785 | 0.25463 | 0.25143 | 0.24825 | 0.24510 | |
| 0.7 | 0.24196 | 0.23885 | 0.23576 | 0.23270 | 0.22965 | 0.22663 | 0.22363 | 0.22065 | 0.21770 | 0.21476 | |
| 0.8 | 0.21186 | 0.20897 | 0.20611 | 0.20327 | 0.20045 | 0.19766 | 0.19489 | 0.19215 | 0.18943 | 0.18673 | |
| 0.9 | 0.18406 | 0.18141 | 0.17879 | 0.17619 | 0.17361 | 0.17106 | 0.16853 | 0.16602 | 0.16354 | 0.16109 | |
| 1.0 | 0.15866 | 0.15625 | 0.15386 | 0.15151 | 0.14917 | 0.14686 | 0.14457 | 0.14231 | 0.14007 | 0.13786 | |
| 1.1 | 0.13567 | 0.13350 | 0.13136 | 0.12924 | 0.12714 | 0.12507 | 0.12302 | 0.12100 | 0.11900 | 0.11702 | |
| 1.2 | 0.11507 | 0.11314 | 0.11123 | 0.10935 | 0.10749 | 0.10565 | 0.10383 | 0.10204 | 0.10027 | 0.09853 | |
| 1.3 | 0.09680 | 0.09510 | 0.09342 | 0.09176 | 0.09012 | 0.08851 | 0.08692 | 0.08534 | 0.08379 | 0.08226 | |
| 1.4 | 0.08076 | 0.07927 | 0.07780 | 0.07636 | 0.07493 | 0.07353 | 0.07215 | 0.07078 | 0.06944 | 0.06811 | |
| 1.5 | 0.06681 | 0.06552 | 0.06426 | 0.06301 | 0.06178 | 0.06057 | 0.05938 | 0.05821 | 0.05705 | 0.05592 | |
| 1.6 | 0.05480 | 0.05370 | 0.05262 | 0.05155 | 0.05050 | 0.04947 | 0.04846 | 0.04746 | 0.04648 | 0.04551 | |
| 1.7 | 0.04457 | 0.04363 | 0.04272 | 0.04182 | 0.04093 | 0.04006 | 0.03920 | 0.03836 | 0.03754 | 0.03673 | |
| 1.8 | 0.03593 | 0.03515 | 0.03438 | 0.03362 | 0.03288 | 0.03216 | 0.03144 | 0.03074 | 0.03005 | 0.02938 | |
| 1.9 | 0.02872 | 0.02807 | 0.02743 | 0.02680 | 0.02619 | 0.02559 | 0.02500 | 0.02442 | 0.02385 | 0.02330 | |
| 2.0 | 0.02275 | 0.02222 | 0.02169 | 0.02118 | 0.02068 | 0.02018 | 0.01970 | 0.01923 | 0.01876 | 0.01831 | |
| 2.1 | 0.01786 | 0.01743 | 0.01700 | 0.01659 | 0.01618 | 0.01578 | 0.01539 | 0.01500 | 0.01463 | 0.01426 | |
| 2.2 | 0.01390 | 0.01355 | 0.01321 | 0.01287 | 0.01255 | 0.01222 | 0.01191 | 0.01160 | 0.01130 | 0.01101 | |
| 2.3 | 0.01072 | 0.01044 | 0.01017 | 0.00990 | 0.00964 | 0.00939 | 0.00914 | 0.00889 | 0.00866 | 0.00842 | |
| 2.4 | 0.00820 | 0.00798 | 0.00776 | 0.00755 | 0.00734 | 0.00714 | 0.00695 | 0.00676 | 0.00657 | 0.00639 | |
| 2.5 | 0.00621 | 0.00604 | 0.00587 | 0.00570 | 0.00554 | 0.00539 | 0.00523 | 0.00508 | 0.00494 | 0.00480 | |
| 2.6 | 0.00466 | 0.00453 | 0.00440 | 0.00427 | 0.00415 | 0.00402 | 0.00391 | 0.00379 | 0.00368 | 0.00357 | |
| 2.7 | 0.00347 | 0.00336 | 0.00326 | 0.00317 | 0.00307 | 0.00298 | 0.00289 | 0.00280 | 0.00272 | 0.00264 | |
| 2.8 | 0.00256 | 0.00248 | 0.00240 | 0.00233 | 0.00226 | 0.00219 | 0.00212 | 0.00205 | 0.00199 | 0.00193 | |
| 2.9 | 0.00187 | 0.00181 | 0.00175 | 0.00169 | 0.00164 | 0.00159 | 0.00154 | 0.00149 | 0.00144 | 0.00139 | |
| 3.0 | 0.00135 | 0.00131 | 0.00126 | 0.00122 | 0.00118 | 0.00114 | 0.00111 | 0.00107 | 0.00104 | 0.00100 | |
Examples of use
A professor's exam scores are approximately distributed normally with mean 80 and standard deviation 5. Only a cumulative from mean table is available.
- What is the probability that a student scores an 82 or less?
- What is the probability that a student scores a 90 or more?
- What is the probability that a student scores a 74 or less?
- Since this table does not include negatives, the process involves the following additional step:
- What is the probability that a student scores between 74 and 82?
- [as in above examples]
- What is the probability that an average of three scores is 82 or less?
References
- ↑ Larson, Ron; Farber, Elizabeth (2004). Elementary Statistics: Picturing the World. 清华大学出版社. p. 214. ISBN 7-302-09723-2.
- ↑ "Cumulative Distribution Function of the Standard Normal Distribution". NIST. Retrieved 5 May 2012.
- ↑ 0.5 + each value in Cumulative from mean table
- ↑ 0.5 - each value in Cumulative from mean (0 to Z) table