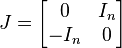Skew-Hamiltonian matrix

In linear algebra, skew-Hamiltonian matrices are special matrices which correspond to skew-symmetric bilinear forms on a symplectic vector space.

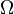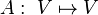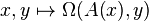Let V be a vector space, equipped with a symplectic form $\Omega$ . Such a space must be even-dimensional. A linear map $A:\; V \mapsto V$ is called a skew-Hamiltonian operator with respect to $\Omega$ if the form $x, y \mapsto \Omega(A(x), y)$ is skew-symmetric.

Choose a basis 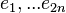$e_1, ... e_{2n}$ in V, such that 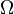$\Omega$ is written as 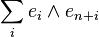$\sum_i e_i \wedge e_{n+i}$ . Then a linear operator is skew-Hamiltonian with respect to 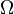$\Omega$ if and only if its matrix A satisfies 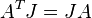$A^T J = J A$ , where J is the skew-symmetric matrix

J= \begin{bmatrix} 0 & I_n \\ -I_n & 0 \\ \end{bmatrix}

and I_n is the 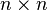$n\times n$ identity matrix.^[1] Such matrices are called skew-Hamiltonian.

The square of a Hamiltonian matrix is skew-Hamiltonian. The converse is also true: every skew-Hamiltonian matrix can be obtained as the square of a Hamiltonian matrix.^[1]^[2]

Notes

1 2 William C. Waterhouse, The structure of alternating-Hamiltonian matrices, Linear Algebra and its Applications, Volume 396, 1 February 2005, Pages 385-390
↑ Heike Faßbender, D. Steven Mackey, Niloufer Mackey and Hongguo Xu Hamiltonian Square Roots of Skew-Hamiltonian Matrices, Linear Algebra and its Applications 287, pp. 125 - 159, 1999

This article is issued from Wikipedia - version of the 6/22/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.