Cycle (graph theory)

A graph with edges colored to illustrate path H-A-B (green), closed path or walk with a repeated vertex B-D-E-F-D-C-B (blue) and a cycle with no repeated edge or vertex H-D-G-H (red)

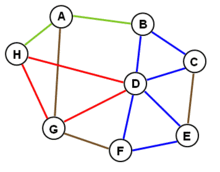
In graph theory, there are several different types of objects called cycles, principally a closed walk and a simple cycle; also, e.g., an element of the cycle space of the graph.

Definitions

A closed walk consists of a sequence of vertices starting and ending at the same vertex, with each two consecutive vertices in the sequence adjacent to each other in the graph. In a directed graph, each edge must be traversed by the walk consistently with its direction: the edge must be oriented from the earlier of two consecutive vertices to the later of the two vertices in the sequence. The choice of starting vertex is not important: traversing the same cyclic sequence of edges from different starting vertices produces the same closed walk.

A simple cycle may be defined either as a closed walk with no repetitions of vertices and edges allowed, other than the repetition of the starting and ending vertex, or as the set of edges in such a walk. The two definitions are equivalent in directed graphs, where simple cycles are also called directed cycles: the cyclic sequence of vertices and edges in a walk is completely determined by the set of edges that it uses. In undirected graphs the set of edges of a cycle can be traversed by a walk in either of two directions, giving two possible directed cycles for every undirected cycle. (For closed walks more generally, in directed or undirected graphs, the multiset of edges does not unambiguously determine the vertex ordering.) A circuit can be a closed walk allowing repetitions of vertices but not edges; however, it can also be a simple cycle, so explicit definition is recommended when it is used.^[1]

In order to maintain a consistent terminology, for the rest of this article, "cycle" means a simple cycle, except where otherwise stated.

Chordless cycles

In this graph the green cycle (A-B-C-D-E-F-A) is chordless whereas the red cycle (G-H-I-J-K-L-G) is not. This is because the edge K-I is a chord.

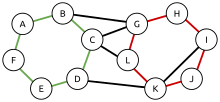
A chordless cycle in a graph, also called a hole or an induced cycle, is a cycle such that no two vertices of the cycle are connected by an edge that does not itself belong to the cycle. An antihole is the complement of a graph hole. Chordless cycles may be used to characterize perfect graphs: by the strong perfect graph theorem, a graph is perfect if and only if none of its holes or antiholes have an odd number of vertices that is greater than three. A chordal graph, a special type of perfect graph, has no holes of any size greater than three.

The girth of a graph is the length of its shortest cycle; this cycle is necessarily chordless. Cages are defined as the smallest regular graphs with given combinations of degree and girth.

A peripheral cycle is a cycle in a graph with the property that every two edges not on the cycle can be connected by a path whose interior vertices avoid the cycle. In a graph that is not formed by adding one edge to a cycle, a peripheral cycle must be an induced cycle.

Cycle space

The term cycle may also refer to an element of the cycle space of a graph. This consists of the edge sets that have even degree at every vertex; it forms a vector space over the two-element finite field. Using methods from algebraic topology, it may be generalized to vector spaces or modules over other rings such as the integers, real numbers, etc. By Veblen's theorem, every element of the cycle space may be formed by as an edge-disjoint union of simple cycles. A cycle basis of the graph is a set of simple cycles that forms a basis of the cycle space.^[2][3]

Cycle detection

The existence of a cycle in directed and undirected graphs can be determined by whether depth-first search (DFS) finds an edge that points to an ancestor of the current vertex (it contains a back edge).^[4] In an undirected graph, finding any already visited vertex will indicate a back edge. All the back edges which DFS skips over are part of cycles.^[5] In the case of undirected graphs, only O(n) time is required to find a cycle in an n-vertex graph, since at most n − 1 edges can be tree edges.

Many topological sorting algorithms will detect cycles too, since those are obstacles for topological order to exist. Also, if a directed graph has been divided into strongly connected components, cycles only exist within the components and not between them, since cycles are strongly connected.^[5]

For directed graphs, Rocha–Thatte Algorithm^[6] is a distributed cycle detection algorithm. Distributed cycle detection algorithms are useful for processing large-scale graphs using a distributed graph processing system on a computer cluster (or supercomputer).

Applications of cycle detection include the use of wait-for graphs to detect deadlocks in concurrent systems.^[7]

Covering graphs by cycles

In his 1736 paper on the Seven Bridges of Königsberg, widely considered to be the birth of graph theory, Leonhard Euler proved that, for a finite undirected graph to have a closed walk that visits each edge exactly once, it is necessary and sufficient that it be connected except for isolated vertices (that is, all edges are contained in one component) and have even degree at each vertex. The corresponding characterization for the existence of a closed walk visiting each edge exactly once in a directed graph is that the graph be strongly connected and have equal numbers of incoming and outgoing edges at each vertex. In either case, the resulting walk is known as an Euler cycle or Euler tour. If a finite undirected graph has even degree at each of its vertices, regardless of whether it is connected, then it is possible to find a set of simple cycles that together cover each edge exactly once: this is Veblen's theorem. ^[8]When a connected graph does not meet the conditions of Euler's theorem, a closed walk of minimum length covering each edge at least once can nevertheless be found in polynomial time by solving the route inspection problem.

The problem of finding a single simple cycle that covers each vertex exactly once, rather than covering the edges, is much harder. Such a cycle is known as a Hamiltonian cycle, and determining whether it exists is NP-complete.^[9] Much research has been published concerning classes of graphs that can be guaranteed to contain Hamiltonian cycles; one example is Ore's theorem that a Hamiltonian cycle can always be found in a graph for which every non-adjacent pair of vertices have degrees summing to at least the total number of vertices in the graph.^[10]

The cycle double cover conjecture states that, for every bridgeless graph, there exists a multiset of simple cycles that covers each edge of the graph exactly twice. Proving that this is true (or finding a counterexample) remains an open problem.^[11]

Graph classes defined by cycles

Several important classes of graphs can be defined by or characterized by their cycles. These include:

• Bipartite graph, a graph without odd cycles.
• Cactus graph, a graph in which every nontrivial biconnected component is a cycle
• Cycle graph, a graph that consists of a single cycle.
• Chordal graph, a graph with no induced cycles of length greater than three
• Directed acyclic graph, a directed graph with no cycles
• Perfect graph, a graph with no induced cycles or their complements of odd length greater than three
• Pseudoforest, a graph in which each connected component has at most one cycle
• Strongly connected graph, a directed graph in which every edge is part of a cycle
• Triangle-free graph, a graph without three-vertex cycles

See also

• Cycle space
• Cycle basis

References