Sierpinski sponge

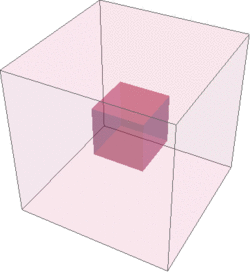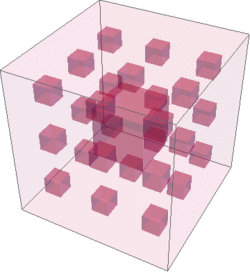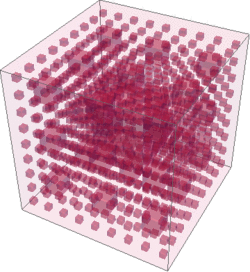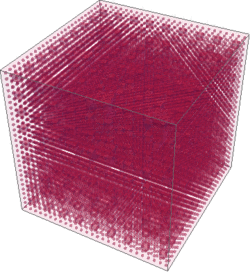
"Jello" plot of the Sierpinski sponge animation through recursion steps. To enable better visibility the darker areas are the holes in the brighter cube. Selected sections cutting the largest cubic cavity parallel to the cube walls show up as the full Sierpinski carpets

The Sierpinski sponge (or Sierpinski cube) is the exact three dimensional extension of the Sierpinski carpet, a fractal where one central cube is removed at each recursion. It is slightly different from the Menger sponge, where seven cubes are removed at each iteration (one in the center and one on each face). Because in the Sierpinski sponge only interior volume is removed, there are no exterior holes and the internal structure cannot be visualized unless the cube is partially transparent.

Because each iteration increases the number of the filling elements grows by $26$ while reducing their size by a factor of 3, the sponge is near-three dimensional with the Hausdorff dimension:

$d_H=\log_3 26 = \ln 26 / \ln 3 \approx 2.965647$

which is more than for the Menger sponge.

In a similar way one may construct other fractal cubes, by removing at each step an arbitrary $N$ -element set of smaller cubes scaled $1/3$ from bigger cubes. The Menger sponge corresponds to the case where the six face cubes and the center cube are removed; while the Cantor cube corresponds to the case where all but the eight corner cubes are removed. Since there are 27 cubes, there are $2^{27}=134217728$ asymptotic objects produced this way, if each of the smaller scaled cubes is treated as different (which corresponds to treating different locations and orientations of the object as different). Most of the cubes constructed in such a way are also strange geometrically in three dimensional space, having the Hausdorff dimension:

$d_{H}=\log _{3}(27-N)=\ln(27-N)/\ln 3$

which is not an integer, unless N is 0 (ie, the unmodified cube), 18, 24, or 26 (in this case the limit will be a single point). (Of course, if N is 27, corresponding to the empty set, the Hausdorff dimension will be $-\infty$ .)

Tree-looking variation of Sierpinski sponge obtained by recursively removing the 8 corner, 6 face-centered and the central cubes (totally 15 cubes) with the fractal dimension $\log _{3}(27-15)\approx 2.261859$
Another tree but Pine-like looking variation obtained by recursively removing 12 edge cubes with the fractal dimension $\log _{3}(27-12)\approx 2.464973$

This article is issued from Wikipedia - version of the 8/15/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.