Shocks and discontinuities (magnetohydrodynamics)
Shocks and discontinuities are transition layers where the plasma properties change from one equilibrium state to another. The relation between the plasma properties on both sides of a shock or a discontinuity can be obtained from the conservative form of the magnetohydrodynamic (MHD) equations, assuming conservation of mass, momentum, energy and of 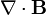 .
.
Rankine-Hugoniot jump conditions for MHD
The jump conditions across a time-independent MHD shock or discontinuity are referred as the Rankine-Hugoniot equations for MHD. In the frame moving with the shock/discontinuity, those jump conditions can be written:
where 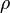 , v, p, B are the plasma density, velocity, (thermal) pressure and magnetic field respectively. The subscripts t and n refer to the tangential and normal components of a vector (with respect to the shock/discontinuity front). The subscripts 1 and 2 refer to the two states of the plasma on each side of the shock/discontinuity
, v, p, B are the plasma density, velocity, (thermal) pressure and magnetic field respectively. The subscripts t and n refer to the tangential and normal components of a vector (with respect to the shock/discontinuity front). The subscripts 1 and 2 refer to the two states of the plasma on each side of the shock/discontinuity
Contact and tangential discontinuities
Contact and tangential discontinuities are transition layers across which there is no particle transport. Thus, in the frame moving with the discontinuity, 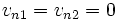 .
.
Contact discontinuities are discontinuities for which the thermal pressure, the magnetic field and the velocity are continuous. Only the mass density and temperature change.
Tangential discontinuities are discontinuities for which the total pressure (sum of the thermal and magnetic pressures) is conserved. The normal component of the magnetic field is identically zero. The density, thermal pressure and tangential component of the magnetic field vector can be discontinuous across the layer.
Shocks
Shocks are transition layers across which there is a transport of particles. There are three types of shocks in MHD: slow-mode, intermediate and fast-mode shocks.
Intermediate shocks are non-compressive (meaning that the plasma density does not change across the shock). A special case of the intermediate shock is referred to as a rotational discontinuity. They are isentropic. All thermodynamic quantities are continuous across the shock, but the tangential component of the magnetic field can "rotate". Intermediate shocks in general however, unlike rotational discontinuities, can have a discontinuity in the pressure.
Slow-mode and fast-mode shocks are compressive and are associated with an increase in entropy. Across slow-mode shock, the tangential component of the magnetic field decreases. Across fast-mode shock it increases.
The type of shocks depend on the relative magnitude of the upstream velocity in the frame moving with the shock with respect to some characteristic speed. Those characteristic speeds, the slow and fast magnetosonic speeds, are related to the Alfvén speed,  and the sonic speed,
and the sonic speed, 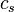 as follows:
as follows:
where 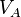 is the Alfvén speed and
is the Alfvén speed and 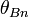 is the angle between the incoming magnetic field and the shock normal vector.
is the angle between the incoming magnetic field and the shock normal vector.
The normal component of the slow shock propagates with velocity 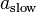 in the frame moving with the upstream plasma, that of the intermediate shock with velocity
in the frame moving with the upstream plasma, that of the intermediate shock with velocity 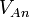 and that of the fast shock with velocity
and that of the fast shock with velocity 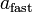 . The fast mode waves have higher phase velocities than the slow mode waves because the density and magnetic field are in phase, whereas the slow mode wave components are out of phase.
. The fast mode waves have higher phase velocities than the slow mode waves because the density and magnetic field are in phase, whereas the slow mode wave components are out of phase.
Example of shocks and discontinuities in space
- The Earth's bow shock, which is the boundary where the solar wind's speed drops due to the presence of Earth's magnetosphere is a fast mode shock. The termination shock is a fast-mode shock due to the interaction of the solar wind with the interstellar medium.
- Magnetic reconnection can happen associated with a slow-mode shock (Petschek or fast magnetic reconnection) in the solar corona.[1]
- The existence of intermediate shocks is still a matter of debate. They may form in MHD simulation, but their stability has not been proven.
- Discontinuities (both contact and tangential) are observed in the solar wind, behind astrophysical shock waves (supernova remnant) or due to the interaction of multiple CME driven shock waves.
- The Earth's magnetopause is generally a tangential discontinuity.[2]
- Coronal Mass Ejections (CMEs) moving at super-Alfvénic speeds are able to drive fast-mode MHD shocks while propagating away from the Sun into the solar wind. Signatures of these shocks have been identified in both radio (as type II radio bursts) and ultraviolet (UV) spectra.[3]
See also
- Magnetohydrodynamics
- Shock wave
- Rankine-Hugoniot equation
- Alfvén wave
- Moreton wave
- List of plasma (physics) applications articles
References
The original research on MHD shock waves can be found in the following papers.
- Herlofson, N. "Magneto-Hydrodynamic Waves in a Compressible Fluid Conductor", Nature, 1950, 165, 1020-1021.
- De Hoffmann, F. & Teller, E. "Magneto-Hydrodynamic Shocks", Physical Review, 1950, 80, 692-703.
- Helfer, H. "Magneto-Hydrodynamic Shock Waves", The Astrophysical Journal, 1953, 117, 177.
- Friedrichs, K. O. "Nonlinear wave motion in magnetohydrodynamics", Los Alamos Sci. Lab. Report LAMS-2105 (Physics), written September 1954, distributed, March 1957. See also the somewhat emended and more available version of this report written jointly with H. Kranzer, Notes on magnetohydrodynamics, VIII, Nonlinear wave motion, AEC Computing and Applied Mathematics Center, Institute of Mathematical Sciences, New York University, Report No. NYO-6486 (1958).
- Marshall, W. "The Structure of Magneto-Hydrodynamic Shock Waves", Proceedings of the Royal Society of London Series A, Mathematical and Physical Sciences, 1955, 233, 367-376.
- Bazer, J. "Resolution of an Initial Shear-Flow Discontinuity in One-Dimensional Hydromagnetic Flow", Astrophysical Journal, vol. 128, p. 686.
- Bazer, J. & Ericson, W. "Hydromagnetic Shocks", The Astrophysical Journal,1959, 129, 758.
- Sears, W. "Some Remarks about Flow past Bodies", Reviews of Modern Physics, 1960, 32, 701-705.
- Grad, H. "Reducible Problems in Magneto-Fluid Dynamic Steady Flows", Reviews of Modern Physics, 1960, 32, 830-847.
Textbook references.
- E. Priest, "Solar magneto-hydrodynamics"(chapter 5), Dordrecht, 1987.
- T. Gombosi "Physics of the Space Environment" (chapter 6), Cambridge University Press, 1998.
- ↑ H. E. Petschek, Magnetic Field Annihilation in The Physics of Solar Flares, Proceedings of the AAS-NASA Symposium held 28–30 October 1963 at the Goddard Space Flight Center, Greenbelt, MD. Edited by Wilmot N. Hess. Washington, DC: National Aeronautics and Space Administration, Science and Technical Information Division, 1964., p.425
- ↑ Magnetopause Belgian Institute for Space Aeronomy
- ↑ S. Mancuso et al., UVCS/SOHO observations of a CME-driven shock: Consequences on ion heating mechanisms behind a coronal shock, Astronomy and Astrophysics, 2002, v.383, p.267-274


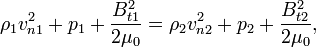
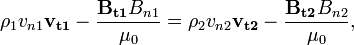

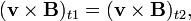
![a_{\mathrm{slow}}^2 = \frac{1}{2} \left[\left(c_s^2 + V_A^2\right)-\sqrt{\left(c_s^2+V_A^2\right)^2-4c_s^2V_{A}^2 \cos^{2} \theta_{Bn}}\,\right],](../I/m/a1fb7ded3b64ee0ee162478fac3a2c02.png)
![a_{\mathrm{fast}}^2 = \frac{1}{2} \left[\left(c_s^2 + V_A^2\right)+\sqrt{\left(c_s^2+V_A^2\right)^2-4c_s^2V_{A}^2 \cos^{2} \theta_{Bn}}\,\right],](../I/m/e1bd68e38264a0817e058f202af3a3f1.png)