Shift-reduce parser
A shift-reduce parser is a class of efficient, table-driven bottom-up parsing methods for computer languages and other notations formally defined by a grammar. The parsing methods most commonly used for parsing programming languages, LR parsing and its variations, are shift-reduce methods.[1] The precedence parsers used before the invention of LR parsing are also shift-reduce methods. All shift-reduce parsers have similar outward effects, in the incremental order in which they build a parse tree or call specific output actions. The outward actions of an LR parser are best understood by ignoring the arcane mathematical details of how LR parser tables are generated, and instead looking at the parser as just some generic shift-reduce method.
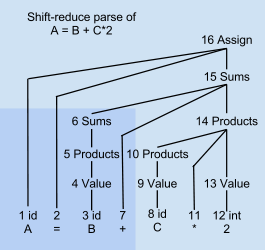
Parse Tree for Example A = B + C*2
A shift-reduce parser scans and parses the input text in one forward pass over the text, without backing up. (That forward direction is generally left-to-right within a line, and top-to-bottom for multi-line inputs.) The parser builds up the parse tree incrementally, bottom up, and left to right, without guessing or backtracking. At every point in this pass, the parser has accumulated a list of subtrees or phrases of the input text that have been already parsed. Those subtrees are not yet joined together because the parser has not yet reached the right end of the syntax pattern that will combine them.
At step 7 in the example parse, only "A = B +" has been parsed. Only the shaded lower-left corner of the parse tree exists. None of the parse tree nodes numbered 8 and above exist yet. Nodes 1, 2, 6, and 7 are the roots of isolated subtrees covering all the items 1..7. Node 1 is variable A, node 2 is the delimiter =, node 6 is the summand B, and node 7 is the operator +. These four root nodes are temporarily held in a parse stack. The remaining unparsed portion of the input stream is "C * 2".
A shift-reduce parser works by doing some combination of Shift steps and Reduce steps, hence the name.
- A Shift step advances in the input stream by one symbol. That shifted symbol becomes a new single-node parse tree.
- A Reduce step applies a completed grammar rule to some of the recent parse trees, joining them together as one tree with a new root symbol.
The parser continues with these steps until all of the input has been consumed and all of the parse trees have been reduced to a single tree representing an entire legal input.
Parse Steps for Example A = B + C*2
At every parse step, the entire input text is divided into parse stack, current lookahead symbol, and remaining unscanned text. The parser's next action is determined by the rightmost stack symbol(s) and the lookahead symbol. The action is read from a table containing all syntactically valid combinations of stack and lookahead symbols.
| Step | Parse Stack | Look Ahead | Unscanned | Parser Action |
|---|---|---|---|---|
| 0 | empty | id | = B + C*2 | Shift |
| 1 | id | = | B + C*2 | Shift |
| 2 | id = | id | + C*2 | Shift |
| 3 | id = id | + | C*2 | Reduce by Value ← id |
| 4 | id = Value | + | C*2 | Reduce by Products ← Value |
| 5 | id = Products | + | C*2 | Reduce by Sums ← Products |
| 6 | id = Sums | + | C*2 | Shift |
| 7 | id = Sums + | id | *2 | Shift |
| 8 | id = Sums + id | * | 2 | Reduce by Value ← id |
| 9 | id = Sums + Value | * | 2 | Reduce by Products ← Value |
| 10 | id = Sums + Products | * | 2 | Shift |
| 11 | id = Sums + Products * | int | eof | Shift |
| 12 | id = Sums + Products * int | eof | Reduce by Value ← int | |
| 13 | id = Sums + Products * Value | eof | Reduce by Products ← Products * Value | |
| 14 | id = Sums + Products | eof | Reduce by Sums ← Sums + Products | |
| 15 | id = Sums | eof | Reduce by Assign ← id = Sums | |
| 16 | Assign | eof | Done |
See [2] for a simpler example.
Grammar for the Example
A grammar is the set of patterns or syntax rules for the input language. It doesn't cover all language rules, such as the size of numbers, or the consistent use of names and their definitions in the context of the whole program. Shift-reduce parsers use a context-free grammar that deals just with local patterns of symbols.
The example grammar used here is a tiny subset of the Java or C language:
- Assign ← id = Sums
- Sums ← Sums + Products
- Sums ← Products
- Products ← Products * Value
- Products ← Value
- Value ← int
- Value ← id
The grammar's terminal symbols are the multi-character symbols or 'tokens' found in the input stream by a lexical scanner. Here these include = + * and int for any integer constant, and id for any identifier name. The grammar doesn't care what the int values or id spellings are, nor does it care about blanks or line breaks. The grammar uses these terminal symbols but does not define them. They are always at the bottom bushy end of the parse tree.
The capitalized terms like Sums are nonterminal symbols. These are names for concepts or patterns in the language. They are defined in the grammar and never occur themselves in the input stream. They are always above the bottom of the parse tree. They only happen as a result of the parser applying some grammar rule. Some nonterminals are defined with two or more rules; these are alternative patterns. Rules can refer back to themselves. This grammar uses recursive rules to handle repeated math operators. Grammars for complete languages use recursive rules to handle lists, parenthesized expressions and nested statements.
Any given computer language can be described by several different grammars. The grammar for a shift-reduce parser must be unambiguous itself, or be augmented by tie-breaking precedence rules. This means there is only one correct way to apply the grammar to a given legal example of the language, resulting in a unique parse tree and a unique sequence of shift/reduce actions for that example.
A table-driven parser has all of its knowledge about the grammar encoded into unchanging data called parser tables. The parser's program code is a simple generic loop that applies unchanged to many grammars and languages. The tables may be worked out by hand for precedence methods. For LR methods, the complex tables are mechanically derived from a grammar by some parser generator tool like Bison.[3] The parser tables are usually much larger than the grammar. In other parsers that are not table-driven, such as recursive descent, each language construct is parsed by a different subroutine, specialized to the syntax of that one construct.
Parser Actions
The shift-reduce parser's efficiency is from doing no backups or backtracking. Its total time scales up linearly with the length of the input and the size of the complete parse tree. Other parser methods that backtrack may take N2 or N3 time when they guess badly.
To avoid guessing, the shift-reduce parser often looks ahead (rightwards) at the next scanned symbol, before deciding what to do with previously scanned symbols. The lexical scanner works one symbol ahead of the rest of the parser. The lookahead symbol is the 'right-hand context' for each parsing decision. (Rarely, two or more lookahead symbols may be utilized, although most practical grammars can be designed to use one lookahead symbol.)
A shift-reduce parser waits until it has scanned and parsed all parts of some construct before committing to what the combined construct is. The parser then acts immediately on the combination instead of waiting any further. In the parse tree example above, the phrase B gets reduced to Value and then to Products and Sums in steps 3-6 as soon as lookahead + is seen, rather than waiting any later to organize those parts of the parse tree. The decisions for how to handle B are based only on what the parser and scanner have already seen, without considering things that appear much later to the right.
Reductions reorganize the most recently parsed things, immediately to the left of the lookahead symbol. So the list of already-parsed things acts like a stack. This parse stack grows rightwards. The base or bottom of the stack is on the left and holds the leftmost, oldest parse fragment. Every reduction step acts only on the rightmost, newest parse fragments. (This accumulative parse stack is very unlike the predictive, leftward-growing parse stack used by top-down parsers.)
When a grammar rule like
- Products ← Products * Value
is applied, the stack top holds the parse trees "... Products * Value". This found instance of the rule's right hand side is called the handle. The reduce step replaces the handle "Products * Value" by the left hand side nonterminal, here a larger Products. If the parser builds complete parse trees, the three trees for inner Products, *, and Value are combined by a new tree root for Products. Otherwise, semantic details from the inner Products and Value are output to some later compiler pass, or are combined and saved in the new Products symbol.[4]
The parser keeps applying reductions to the top of the parse stack for as long as it keeps finding newly completed examples of grammar rules there. When no more rules can be applied, the parser then shifts the lookahead symbol onto the parse stack, scans a new lookahead symbol, and tries again.
Types of Shift-Reduce Parsers
The parser tables show what to do next, for every legal combination of topmost parse stack symbols and lookahead symbol. That next action must be unique; either shift, or reduce, but not both. (This implies some further limitations on the grammar, beyond being unambiguous.) The table details vary greatly between different types of shift-reduce parsers.
In precedence parsers, the right end of handles are found by comparing the precedence level or grammar tightness of the top stack symbols to that of the lookahead symbol. In the example above, int and id belong to inner grammar levels compared to the statement delimiter ;. So int and id are both considered to be higher precedence than ; and should be reduced to something else whenever followed by ;. There are different varieties of precedence parsers, each with different ways of finding the handle's left end and choosing the correct rule to apply:
- Operator-precedence parser, a very simple numerical method that works for expressions but not general program syntax.
- Simple precedence parser, uses one large MxN table to find right and left ends. Used in PL360.[5] Does not handle common programming languages.
- Weak precedence parser, uses the precedence table only to find handles' right ends. Handles more grammars than simple precedence.[6]
- Extended precedence parser.
- Mixed Strategy Precedence parser, used by the original version of XPL. Extends the "doubles", inherent in any precedence recognizer, to include "triples". Less powerful than SLR. Generally has very large tables, even for relatively small languages, such as XPL itself, on account of the great many "triples" which are required to recognize grammars outside the limits imposed by precedence methods.[7]
Precedence parsers are limited in the grammars they can handle. They ignore most of the parse stack when making decisions. They consider only the names of the topmost symbols, not the full context of where in the grammar those symbols are now appearing. Precedence requires that similar-looking symbol combinations must be parsed and used in identical ways throughout the grammar, however those combinations happen, regardless of context.
LR parsers are a more flexible form of shift-reduce parsing, handling many more grammars.[8] LR parsers function like a state machine, performing a state transition for each shift or reduce action. These employ a stack where the current state is pushed (down) by shift actions. This stack is then popped (up) by reduce actions. This mechanism allows the LR parser to handle all deterministic context-free grammars, a superset of precedence grammars. The LR parser is fully implemented by the Canonical LR parser. The Look-Ahead LR and Simple LR parsers implement simplified variants of it that have significantly reduced memory requirements.[9][10] Recent research has identified methods by which canonical LR parsers may be implemented with dramatically reduced table requirements over Knuth's table-building algorithm.[11]
General LR-type Parser Processing
Whether LR, LALR or SLR, the basic state machine is the same; only the tables are different, and these tables are almost always mechanically generated. Additionally, these tables are usually implemented such that a REDUCE results in a CALL to a closed subroutine which is external to the state machine and which performs a function which is implied by the semantics of the grammar rule which is being REDUCEd. Therefore, the parser is partitioned into an invariant state machine part, and a variant semantics part. This fundamental distinction encourages the development of high-quality parsers which are exceptionally reliable.
Given a specific stack state and lookahead symbol, there are precisely four possible actions, ERROR, SHIFT, REDUCE, and STOP (hereinafter referred to as configurations). The presence of a dot, •, in a configuration represents the current lookahead position, with the lookahead symbol shown to the right of the dot (and which always corresponds to a terminal symbol), and the current stack state to the left of the dot (and which usually corresponds to a nonterminal symbol).
For practical reasons, certainly including higher performance, the tables are usually extended by a somewhat large, auxiliary array of two-bit symbols, obviously compressed into four two-bit symbols, a byte, for efficient accessing on byte-oriented machines, often encoded as:
- 00b represents ERROR
- 01b represents SHIFT
- 10b represents REDUCE
- 11b represents STOP
(STOP being a special case of SHIFT). The entire array generally includes mostly ERROR configurations, a grammar-defined number of SHIFT and REDUCE configurations, and one STOP configuration.
In programming systems which support the specification of values in quaternary numeral system (base 4, two bits per quaternary digit), such as XPL, these are coded as:
- "(2)…0…" represents ERROR
- "(2)…1…" represents SHIFT
- "(2)…2…" represents REDUCE
- "(2)…3…" represents STOP
Obviously, the SHIFT and the REDUCE tables are implemented separately from the array, and significant efficiencies may be achieved through optimal "decomposition" of those SHIFT and REDUCE tables (ERROR and STOP need no tables). The auxiliary array need be "probed" only for the instant state and lookahead symbol, and only for a SHIFT or REDUCE are the tables accessed, thereby avoiding unnecessary "probing" of, potentially, a large portion of the tables for a "match" on the state and the lookahead symbol (this obviously depends upon the degree to which the tables have been "decomposed", as the array is "full", whereas the tables may be very "sparse").
The SHIFT and REDUCE configurations are obvious, from the basic definition of a SHIFT-REDUCE parser.
STOP, then, represents a configuration where the state at the top of the stack and the lookahead terminal symbol is within the subject grammar, and represents the ending of the program:
- ⊥ <program> • ⊥
it being impossible to SHIFT beyond the final ⊥ so as to reach:
- ⊥ <program> ⊥ •
ERROR, then, represents a configuration where the state at the top of the stack, and the lookahead terminal symbol is not within the subject grammar. This presents an opportunity to invoke an error recovery procedure, perhaps, in its most simplistic form, to discard the lookahead terminal symbol and to read the next terminal symbol, but many other programmed actions are certainly possible, including pruning the stack, or discarding the lookahead terminal symbol and pruning the stack (and in a pathological case, it is usually possible to obtain
- ⊥ <program> • ⊥
where <program> consists only of a "null statement").
In most cases, the stack is purposely pre-loaded, that is, initialized, with
- ⊥ • <program> ⊥
whereby the initial ⊥ is assumed to have already been recognized. This, then, represents the beginning of the program, and, thereby, avoids having a separate START configuration, and which is, conceptually,
- • ⊥ <program> ⊥
⊥ is a special pseudo-terminal symbol mechanically added to the grammar, just as <program> is a special pseudo-nonterminal symbol mechanically added to the grammar (if the programmer did not explicitly include <program> in the grammar, then <program> would be automatically added to the grammar on the programmer's behalf).
Clearly, such a parser has precisely one (implicit) START configuration and one (explicit) STOP configuration, but it can, and usually does have hundreds of SHIFT and REDUCE configurations, and perhaps thousands of ERROR configurations.
References
- ↑ Compilers: Principles, Techniques, and Tools (2nd Edition), by Alfred Aho, Monica Lam, Ravi Sethi, and Jeffrey Ullman, Prentice Hall 2006.
- ↑ http://dragonbook.stanford.edu/lecture-notes/Stanford-CS143/08-Bottom-Up-Parsing.pdf
- ↑ Flex & Bison: Text Processing Tools, by John Levine, O'Reilly Media 2009.
- ↑ Crafting and Compiler, by Charlese Fischer, Ron Cytron, and Richard LeBlanc, Addison Wesley 2009.
- ↑ PL360 - A Programming Language for the 360 Computers, by Niklaus Wirth, J. ACM 15:1 1968.
- ↑ The Theory of Parsing, Translation, and Compiling, Volume 1: Parsing, by Alfred Aho and Jeffrey Ullman, Prentice Hall 1972.
- ↑ A Compiler Generator, by W. McKeeman, J Horning, and D Wortman, Prentice Hall 1970.
- ↑ Knuth, D. E. (July 1965). "On the translation of languages from left to right" (PDF). Information and Control. 8 (6): 607–639. doi:10.1016/S0019-9958(65)90426-2. Retrieved 29 May 2011.
- ↑ Practical Translators for LR(k) Languages, by Frank DeRemer, MIT PhD dissertation 1969.
- ↑ Simple LR(k) Grammars, by Frank DeRemer, Comm. ACM 14:7 1971.
- ↑ X. Chen, Measuring and extending LR(1) parsing, University of Hawaii PhD dissertation, 2009.