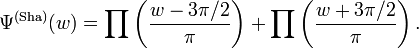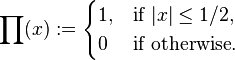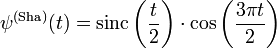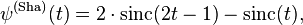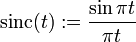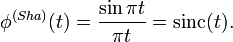Shannon wavelet

In functional analysis, a Shannon wavelet may be either of real or complex type. Signal analysis by ideal bandpass filters defines a decomposition known as Shannon wavelets (or sinc wavelets). The Haar and sinc systems are Fourier duals of each other.

Real Shannon wavelet

Real Shannon wavelet

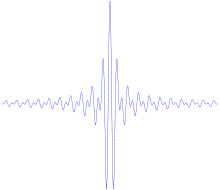
The Fourier transform of the Shannon mother wavelet is given by:

\Psi^{(\operatorname{Sha}) }(w) = \prod \left( \frac {w- 3 \pi /2} {\pi}\right)+\prod \left( \frac {w+ 3 \pi /2} {\pi}\right).

where the (normalised) gate function is defined by

\prod ( x):= \begin{cases} 1, & \mbox{if } {|x| \le 1/2}, \\ 0 & \mbox{if } \mbox{otherwise}. \\ \end{cases}

The analytical expression of the real Shannon wavelet can be found by taking the inverse Fourier transform:

\psi^{(\operatorname{Sha}) }(t) = \operatorname{sinc} \left( \frac {t} {2}\right)\cdot \cos \left( \frac {3 \pi t} {2}\right)

or alternatively as

\psi^{(\operatorname{Sha})}(t)=2 \cdot \operatorname{sinc}(2t - 1)-\operatorname{sinc}(t),

where

\operatorname{sinc}(t):= \frac {\sin {\pi t}} {\pi t}

is the usual sinc function that appears in Shannon sampling theorem.

This wavelet belongs to the 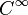C^\infty-class of differentiability, but it decreases slowly at infinity and has no bounded support, since band-limited signals cannot be time-limited.

The scaling function for the Shannon MRA (or Sinc-MRA) is given by the sample function:

\phi^{(Sha)}(t)= \frac {\sin \pi t} {\pi t} = \operatorname{sinc}(t).

Complex Shannon wavelet

In the case of complex continuous wavelet, the Shannon wavelet is defined by

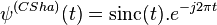\psi^{(CSha) }(t)=\operatorname{sinc}(t).e^{-j2 \pi t},

References

This article is issued from Wikipedia - version of the 3/25/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.