Sellmeier equation

The Sellmeier equation is an empirical relationship between refractive index and wavelength for a particular transparent medium. The equation is used to determine the dispersion of light in the medium.
It was first proposed in 1871 by Wilhelm Sellmeier and was a development of the work of Augustin Cauchy on Cauchy's equation for modelling dispersion.
The equation
The usual form of the equation for glasses is
where n is the refractive index, λ is the wavelength, and B1,2,3 and C1,2,3 are experimentally determined Sellmeier coefficients.[1] These coefficients are usually quoted for λ in micrometres. Note that this λ is the vacuum wavelength, not that in the material itself, which is λ/n(λ). A different form of the equation is sometimes used for certain types of materials, e.g. crystals.
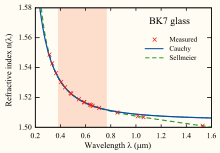
As an example, the coefficients for a common borosilicate crown glass known as BK7 are shown below:
| Coefficient | Value |
|---|---|
| B1 | 1.03961212 |
| B2 | 0.231792344 |
| B3 | 1.01046945 |
| C1 | 6.00069867×10−3 μm2 |
| C2 | 2.00179144×10−2 μm2 |
| C3 | 1.03560653×102 μm2 |
The Sellmeier coefficients for many common optical materials can be found in the online database of RefractiveIndex.info.
For common optical glasses, the refractive index calculated with the three-term Sellmeier equation deviates from the actual refractive index by less than 5×10−6 over the wavelengths' range[2] of 365 nm to 2.3 µm, which is of the order of the homogeneity of a glass sample.[3] Additional terms are sometimes added to make the calculation even more precise. In its most general form, the Sellmeier equation is given as
with each term of the sum representing an absorption resonance of strength Bi at a wavelength √Ci. For example, the coefficients for BK7 above correspond to two absorption resonances in the ultraviolet, and one in the mid-infrared region. Close to each absorption peak, the equation gives non-physical values of n2 = ±∞, and in these wavelength regions a more precise model of dispersion such as Helmholtz's must be used.
If all terms are specified for a material, at long wavelengths far from the absorption peaks the value of n tends to
where εr is the relative dielectric constant of the medium.
The Sellmeier equation can also be given in another form:[4]
Here the coefficient A is an approximation of the short-wavelength (e.g., ultraviolet) absorption contributions to the refractive index at longer wavelengths. Other variants of the Sellmeier equation exist that can account for a material's refractive index change due to temperature, pressure, and other parameters.
Coefficients
| Material | B1 | B2 | B3 | C1, µm2 | C2, µm2 | C3, µm2 |
|---|---|---|---|---|---|---|
| borosilicate crown glass (known as BK7) | 1.03961212 | 0.231792344 | 1.01046945 | 6.00069867×10−3 | 2.00179144×10−2 | 103.560653 |
| sapphire (for ordinary wave) | 1.43134930 | 0.65054713 | 5.3414021 | 5.2799261×10−3 | 1.42382647×10−2 | 325.017834 |
| sapphire (for extraordinary wave) | 1.5039759 | 0.55069141 | 6.5927379 | 5.48041129×10−3 | 1.47994281×10−2 | 402.89514 |
| fused silica | 0.696166300 | 0.407942600 | 0.897479400 | 4.67914826×10−3 | 1.35120631×10−2 | 97.9340025 |
See also
References
- ↑ Refractive index and dispersion. Schott technical information document TIE-29 (2007).
- ↑ http://oharacorp.com/o2.html
- ↑ http://oharacorp.com/o7.html
- ↑ Ghosh, Gorachand. "Sellmeier Coefficients and Dispersion of Thermo-Optic coefficients for some optical glasses" (PDF). Applied Optics. Retrieved 18 February 2014.
- ↑ http://www.lacroixoptical.com/sites/default/files/content/LaCroix%20Dynamic%20Material%20Selection%20Data%20Tool%20vJanuary%202015.xlsm
- W. Sellmeier, Zur Erklärung der abnormen Farbenfolge im Spectrum einiger Substanzen, Annalen der Physik und Chemie 219, 272-282 (1871).
External links
- RefractiveIndex.INFO Refractive index database featuring Sellmeier coefficients for many hundreds of materials.
- A browser-based calculator giving refractive index from Sellmeier coefficients.
- Annalen der Physik - free Access, digitized by the French national library
- Sellmeier coefficients for 356 glasses from Ohara, Hoya, and Schott