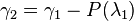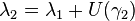Second-generation wavelet transform

In signal processing, the second-generation wavelet transform (SGWT) is a wavelet transform where the filters (or even the represented wavelets) are not designed explicitly, but the transform consists of the application of the Lifting scheme. Actually, the sequence of lifting steps could be converted to a regular discrete wavelet transform, but this is unnecessary because both design and application is made via the lifting scheme. This means that they are not designed in the frequency domain, as they are usually in the classical (so to speak first generation) transforms such as the DWT and CWT). The idea of moving away from the Fourier domain was introduced independently by David Donoho and Harten in the early 1990s.

Calculating transform

The input signal 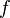$f$ is split into odd 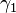$\gamma _1$ and even 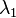$\lambda _1$ samples using shifting and downsampling. The detail coefficients 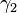$\gamma _2$ are then interpolated using the values of 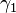$\gamma _1$ and the prediction operator on the even values:

\gamma _2 = \gamma _1 - P(\lambda _1 ) \,

The next stage (known as the updating operator) alters the approximation coefficients using the detailed ones:

\lambda _2 = \lambda _1 + U(\gamma _2 ) \,

The functions prediction operator 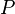$P$ and updating operator 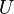$U$ effectively define the wavelet used for decomposition. For certain wavelets the lifting steps (interpolating and updating) are repeated several times before the result is produced.

The idea can be expanded (as used in the DWT) to create a filter bank with a number of levels. The variable tree used in wavelet packet decomposition can also be used.

Advantages

The SGWT has a number of advantages over the classical wavelet transform in that it is quicker to compute (by a factor of 2) and it can be used to generate a multiresolution analysis that does not fit a uniform grid. Using a priori information the grid can be designed to allow the best analysis of the signal to be made. The transform can be modified locally while preserving invertibility; it can even adapt to some extent to the transformed signal.

References

Wim Sweldens: Second-Generation Wavelets: Theory and Application

This article is issued from Wikipedia - version of the 4/29/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.