Saturated measure
In mathematics, a measure is said to be saturated if every locally measurable set is also measurable.[1] A set  , not necessarily measurable, is said to be locally measurable if for every measurable set
, not necessarily measurable, is said to be locally measurable if for every measurable set  of finite measure,
of finite measure, 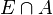 is measurable.
is measurable.  -finite measures, and measures arising as the restriction of outer measures, are saturated.
-finite measures, and measures arising as the restriction of outer measures, are saturated.
References
- ↑ Bogachev, Vladmir (2007). Measure Theory Volume 2. Springer. ISBN 978-3-540-34513-8.
This article is issued from Wikipedia - version of the 8/31/2012. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.