Hoover index

The Hoover index, also known as the Robin Hood index, but better known as the Schutz index, is a measure of income metrics. It is equal to the portion of the total community income that would have to be redistributed (taken from the richer half of the population and given to the poorer half) for there to be income uniformity.

It can be graphically represented as the longest vertical distance between the Lorenz curve, or the cumulative portion of the total income held below a certain income percentile, and the 45 degree line representing perfect equality.

The Hoover index is typically used in applications related to socio-economic class (SES) and health. It is conceptually one of the simplest inequality indices used in econometrics. A better known inequality measure is the Gini coefficient which is also based on the Lorenz curve.

Computation

For the formula, a notation[1] is used, where the amount 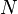N of quantiles only appears as upper border of summations. Thus, inequities can be computed for quantiles with different widths 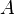A. For example, 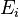E_i could be the income in the quantile #i and 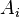A_i could be the amount (absolute or relative) of earners in the quantile #i. E_\text{total} then would be the sum of incomes of all 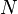N quantiles and A_\text{total} would be the sum of the income earners in all 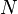N quantiles.

Computation of the Robin Hood index 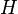H:

H = {\frac{1}{2}} \sum_{i=1}^N \left| {\frac{{E}_i}{{E}_\text{total}}} - {\frac{{A}_i}{{A}_\text{total}}} \right|.

For comparison,[2] here also the computation of the symmetrized Theil index T_s is given:

T_s = {\frac{1}{2}} \sum_{i=1}^N \ln{\frac{{E}_i}{{A}_i}} \left({\frac{{E}_i}{{E}_\text{total}}} - {\frac{{A}_i}{{A}_\text{total}}} \right).

Both formulas can be used in spreadsheet computations.

See also

Notes

  1. ↑ The notation using E and A follows the notation of a small calculation published by Lionnel Maugis: Inequality Measures in Mathematical Programming for the Air Traffic Flow Management Problem with En-Route Capacities (für IFORS 96), 1996
  2. ↑ For an explanation of the comparison with Henri Theil's index see: Theil index

Further reading

External links

This article is issued from Wikipedia - version of the 11/2/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.