Turn (geometry)
| Turn | |
|---|---|
| Unit of | Plane angle |
| Symbol | tr or pla |
| Unit conversions | |
| 1 tr in ... | ... is equal to ... |
| radians | 6.283185307179586... rad |
| radians | 2π rad |
| degrees | 360° |
| gons | 400g |

A turn is a unit of plane angle measurement equal to 2π radians, 360° or 400 gon. A turn is also referred to as a revolution or complete rotation or full circle or cycle or rev or rot.
A turn can be subdivided in many different ways: into half turns, quarter turns, centiturns, milliturns, binary angles, points etc.
Subdivision of turns
A turn can be divided in 100 centiturns or 1000 milliturns, with each milliturn corresponding to an angle of 0.36°, which can also be written as 21′ 36″. A protractor divided in centiturns is normally called a percentage protractor.
Binary fractions of a turn are also used. Sailors have traditionally divided a turn into 32 compass points. The binary degree, also known as the binary radian (or brad), is 1⁄256 turn.[1] The binary degree is used in computing so that an angle can be represented to the maximum possible precision in a single byte. Other measures of angle used in computing may be based on dividing one whole turn into 2n equal parts for other values of n.[2]
The notion of turn is commonly used for planar rotations. Two special rotations have acquired appellations of their own: a rotation through 180° is commonly referred to as a half-turn (π radians),[3] a rotation through 90° is referred to as a quarter-turn.
History
The word turn originates via Latin and French from the Greek word τόρνος (tornos – a lathe).
In 1697, David Gregory used π/ρ (pi over rho) to denote the perimeter of a circle (i.e., the circumference) divided by its radius.[4][5] However, earlier in 1647, William Oughtred had used δ/π (delta over pi) for the ratio of the diameter to perimeter. The first use of the symbol π on its own with its present meaning (of perimeter divided by diameter) was in 1706 by the Welsh mathematician William Jones.[6] Euler adopted the symbol with that meaning in 1737, leading to its widespread use.
Percentage protractors have existed since 1922,[7] but the terms centiturns and milliturns were introduced much later by Sir Fred Hoyle.[8]
The German standard DIN 1315 (1974-03) proposed the unit symbol pla (from Latin: plenus angulus "full angle") for turns.[9][10] Since 2011, the HP 39gII and HP Prime support the unit symbol tr for turns. In 2016, support for turns was also added to newRPL for the HP 50g.[11]
Unit conversion
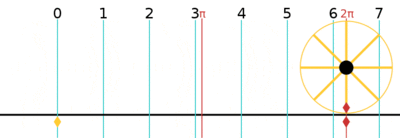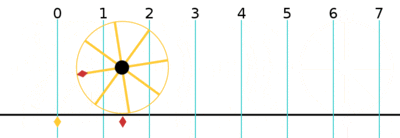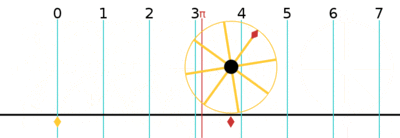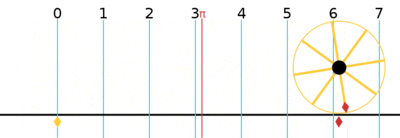
One turn is equal to 2π (≈ 6.283185307179586)[12] radians.
| Turns | Radians | Degrees | Gradians (Gons) |
|---|---|---|---|
| 0 turn | 0 rad | 0° | 0g |
| 1/24 turn | π/12 rad | 15° | 16 2/3g |
| 1/12 turn | π/6 rad | 30° | 33 1/3g |
| 1/10 turn | π/5 rad | 36° | 40g |
| 1/8 turn | π/4 rad | 45° | 50g |
| 1/2π turn | 1 rad | c. 57.3° | c. 63.7g |
| 1/6 turn | π/3 rad | 60° | 66 2/3g |
| 1/5 turn | 2π/5 rad | 72° | 80g |
| 1/4 turn | π/2 rad | 90° | 100g |
| 1/3 turn | 2π/3 rad | 120° | 133 1/3g |
| 2/5 turn | 4π/5 rad | 144° | 160g |
| 1/2 turn | π rad | 180° | 200g |
| 3/4 turn | 3π/2 rad | 270° | 300g |
| 1 turn | 2π rad | 360° | 400g |
Tau proposal

In 1958, Albert Eagle proposed τ as a symbol for 1/2π, because π resembles two τ symbols conjoined (ττ).[13]
In 2001, Robert Palais proposed using the number of radians in a turn as the fundamental circle constant instead of π, which amounts to the number of radians in half a turn, in order to make mathematics simpler and more intuitive, using a "pi with three legs" symbol to denote the constant ( = 2π).[14]
In 2010, Michael Hartl proposed to use the Greek letter tau (τ) instead of pi (π) for two reasons. First, τ is the number of radians in one turn, which allows fractions of a turn to be expressed more directly: for instance, a 3/4 turn would be represented as 3/4τ rad instead of 3/2π rad. Second, τ visually resembles π, whose association with the circle constant is unavoidable.[15] Hartl's Tau Manifesto gives many examples of formulas that are simpler if tau is used instead of pi.[16][17][18]
Examples of use
- As an angular unit, the turn or revolution is particularly useful for large angles, such as in connection with electromagnetic coils and rotating objects. See also winding number.
- The angular speed of rotating machinery, such as automobile engines, is commonly measured in revolutions per minute or RPM.
- Turn is used in complex dynamics for measure of external and internal angles. The sum of external angles of a polygon equals one turn. Angle doubling map is used.
- Pie charts illustrate proportions of a whole as fractions of a turn. Each one percent is shown as an angle of one centiturn.
Kinematics of turns
In kinematics, a turn is a rotation less than a full revolution. A turn may be represented in a mathematical model that uses expressions of complex numbers or quaternions. In the complex plane every non-zero number has a polar coordinate expression z = r cis(a) = r cos(a) + ri sin(a) where r > 0 and a is in [0, 2π). A turn of the complex plane arises from multiplying z = x + iy by an element u = ebi that lies on the unit circle:
- z ↦ uz.
Frank Morley consistently referred to elements of the unit circle as turns in the book Inversive Geometry, (1933) which he coauthored with his son Frank Vigor Morley.[19]
The Latin term for turn is versor, which is a quaternion that can be visualized as an arc of a great circle. The product of two versors can be compared to a spherical triangle where two sides add to the third. For the kinematics of rotation in three dimensions, see quaternions and spatial rotation.
See also
- Angle of rotation
- Revolutions per minute
- Repeating circle
- Spat (unit)
- Unit interval
- Turn (rational trigonometry)
- Spread
Notes and references
- ↑ "ooPIC Programmer's Guide". www.oopic.com.
- ↑ Hargreaves, Shawn. "Angles, integers, and modulo arithmetic". blogs.msdn.com.
- ↑ "Half Turn, Reflection in Point". cut-the-knot.org.
- ↑ Beckmann, Petr (1989). A History of Pi. Barnes & Noble Publishing.
- ↑ Schwartzman, Steven (1994). The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English. The Mathematical Association of America. p. 165.
- ↑ "Pi through the ages".
- ↑ Croxton, Frederick E. (1922). "A Percentage Protractor". Journal of the American Statistical Association. 18: 108–109. doi:10.1080/01621459.1922.10502455.
- ↑ Hoyle, Fred (1962). Astronomy. London: Macdonald.
- ↑ German, Sigmar; Drath, Peter (2013-03-13) [1979]. Handbuch SI-Einheiten: Definition, Realisierung, Bewahrung und Weitergabe der SI-Einheiten, Grundlagen der Präzisionsmeßtechnik (in German) (1 ed.). Friedrich Vieweg & Sohn Verlagsgesellschaft mbH, reprint: Springer-Verlag. ISBN 3322836061. 978-3-528-08441-7, 9783322836069. Retrieved 2015-08-14.
- ↑ Kurzweil, Peter (2013-03-09) [1999]. Das Vieweg Einheiten-Lexikon: Formeln und Begriffe aus Physik, Chemie und Technik (in German) (1 ed.). Vieweg, reprint: Springer-Verlag. doi:10.1007/978-3-322-92920-4. ISBN 3322929205. 978-3-322-92921-1. Retrieved 2015-08-14.
- ↑ http://www.hpmuseum.org/forum/thread-4783-post-55836.html#pid55836
- ↑ Sequence
 A019692
A019692 - ↑ Eagle, Albert (1958). The Elliptic Functions as They Should Be: An Account, with Applications, of the Functions in a New Canonical Form. Cambridge, England: Galloway and Porter.
- ↑ Palais, Robert (2001). "Pi is Wrong" (PDF). The Mathematical Intelligencer. New York, USA: Springer-Verlag. 23 (3): 7–8. doi:10.1007/bf03026846.
- ↑ Hartl, Michael (2013-03-14). "The Tau Manifesto". Retrieved 2013-09-14.
- ↑ Aron, Jacob (2011-01-08). "Interview: Michael Hartl: It's time to kill off pi". New Scientist. 209 (2794): 23. Bibcode:2011NewSc.209...23A. doi:10.1016/S0262-4079(11)60036-5.
- ↑ Landau, Elizabeth (2011-03-14). "On Pi Day, is 'pi' under attack?". cnn.com.
- ↑ "Why Tau Trumps Pi". Scientific American. 2014-06-25. Retrieved 2015-03-20.
- ↑ Morley, Frank; Morley, Frank Vigor (2014) [1933]. Inversive Geometry. Boston, USA; New York, USA: Ginn and Company, reprint: Courier Corporation, Dover Publications. ISBN 978-0-486-49339-8. 0-486-49339-3. Retrieved 2015-10-17.
External links
- Palais, Robert (2001). "Pi is Wrong" (PDF). The Mathematical Intelligencer. New York, USA: Springer-Verlag. 23 (3): 7–8. doi:10.1007/bf03026846.