Pseudoideal

In the theory of partially ordered sets, a pseudoideal is a subset characterized by a bounding operator LU.

Basic definitions

LU(A) is the set of all lower bounds of the set of all upper bounds of the subset A of a partially ordered set.

A subset I of a partially ordered set (P,≤) is a Doyle pseudoideal, if the following condition holds:

For every finite subset S of P that has a supremum in P, S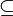 $\subseteq$ I implies that LU(S) 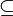$\subseteq$ I.

A subset I of a partially ordered set (P,≤) is a pseudoideal, if the following condition holds:

For every subset S of P having at most two elements that has a supremum in P, S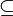 $\subseteq$ I implies that LU(S) 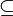$\subseteq$ I.

Every Frink ideal I is a Doyle pseudoideal.
A subset I of a lattice (P,≤) is a Doyle pseudoideal if and only if it is a lower set that is closed under finite joins (suprema).

Abian, A., Amin, W. A. (1990) "Existence of prime ideals and ultrafilters in partially ordered sets", Czechoslovak Math. J., 40: 159–163.
Doyle, W.(1950) "An arithmetical theorem for partially ordered sets", Bulletin of the American Mathematical Society, 56: 366.
Niederle, J. (2006) "Ideals in ordered sets", Rendiconti del Circolo Matematico di Palermo 55: 287–295.

This article is issued from Wikipedia - version of the 4/9/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.