Path tracing

Path tracing is a computer graphics Monte Carlo method of rendering images of three-dimensional scenes such that the global illumination is faithful to reality. Fundamentally, the algorithm is integrating over all the illuminance arriving to a single point on the surface of an object. This illuminance is then reduced by a surface reflectance function (BRDF) to determine how much of it will go towards the viewpoint camera. This integration procedure is repeated for every pixel in the output image. When combined with physically accurate models of surfaces, accurate models of real light sources (light bulbs), and optically-correct cameras, path tracing can produce still images that are indistinguishable from photographs.
Path tracing naturally simulates many effects that have to be specifically added to other methods (conventional ray tracing or scanline rendering), such as soft shadows, depth of field, motion blur, caustics, ambient occlusion, and indirect lighting. Implementation of a renderer including these effects is correspondingly simpler. An extended version of the algorithm is realized by volumetric path tracing, which considers the light scattering of a scene.
Due to its accuracy and unbiased nature, path tracing is used to generate reference images when testing the quality of other rendering algorithms. In order to get high quality images from path tracing, a large number of rays must be traced to avoid visible noisy artifacts.
History
The rendering equation and its use in computer graphics was presented by James Kajiya in 1986. Path Tracing was introduced then as an algorithm to find a numerical solution to the integral of the rendering equation. A decade later, Lafortune suggested many refinements, including bidirectional path tracing.
Metropolis light transport, a method of perturbing previously found paths in order to increase performance for difficult scenes, was introduced in 1997 by Eric Veach and Leonidas J. Guibas.
More recently, CPUs and GPUs have become powerful enough to render images more quickly, causing more widespread interest in path tracing algorithms. Tim Purcell first presented a global illumination algorithm running on a GPU in 2002. In February 2009 Austin Robison of Nvidia demonstrated the first commercial implementation of a path tracer running on a GPU , and other implementations have followed, such as that of Vladimir Koylazov in August 2009. This was aided by the maturing of GPGPU programming toolkits such as CUDA and OpenCL and GPU ray tracing SDKs such as OptiX.
Description
Kajiya's rendering equation adheres to three particular principles of optics; the Principle of global illumination, the Principle of Equivalence (reflected light is equivalent to emitted light), and the Principle of Direction (reflected light and scattered light have a direction).
In the real world, objects and surfaces are visible due to the fact that they are reflecting light. This reflected light then illuminates other objects in turn. From that simple observation, two principles follow.
I. For a given indoor scene, every object in the room must contribute illumination to every other object.
II. Second, there is no distinction to be made between illumination emitted from a light source and illumination reflected from a surface.
Invented in 1984, a rather different method called radiosity was faithful to both principles. However, radiosity relates the total illuminance falling on a surface with a uniform luminance that leaves the surface. This forced all surfaces to be Lambertian, or "perfectly diffuse". While radiosity received a lot of attention at its invocation, perfectly diffuse surfaces do not exist in the real world. The realization that scattering from a surface depends on both incoming and outgoing directions is the key principle behind the Bidirectional reflectance distribution function (BRDF)]. This direction dependence was a focus of research resulting in the publication of important ideas throughout the 1990s, since accounting for direction always exacted a price of steep increases in calculation times on desktop computers. Principle III follows.
III. The illumination coming from surfaces must scatter in a particular direction that is some function of the incoming direction of the arriving illumination, and the outgoing direction being sampled.
Kajiya's equation is a complete summary of these three principles, and path tracing, which approximates a solution to the equation, remains faithful to them in its implementation. There are other principles of optics which are not the focus of Kajiya's equation, and therefore are often difficult or incorrectly simulated by the algorithm. Path Tracing is confounded by optical phenomena not contained in the three principles. For example,
- Bright, sharp caustics; radiance scales by the density of illuminance in space.
- Subsurface scattering; a violation of principle III above.
- Chromatic aberration, fluorescence, iridescence; light is a spectrum of frequencies.
Algorithm
The following pseudocode is a procedure for performing naive path tracing. This function calculates a single sample of a pixel, where only the Gathering Path is considered.
Color TracePath(Ray r, depth) {
if (depth == MaxDepth) {
return Black; // Bounced enough times.
}
r.FindNearestObject();
if (r.hitSomething == false) {
return Black; // Nothing was hit.
}
Material m = r.thingHit->material;
Color emittance = m.emittance;
// Pick a random direction from here and keep going.
Ray newRay;
newRay.origin = r.pointWhereObjWasHit;
newRay.direction = RandomUnitVectorInHemisphereOf(r.normalWhereObjWasHit); // This is NOT a cosine-weighted distribution!
// Compute the BRDF for this ray (assuming Lambertian reflection)
float cos_theta = DotProduct(newRay.direction, r.normalWhereObjWasHit);
Color BRDF = 2 * m.reflectance * cos_theta;
Color reflected = TracePath(newRay, depth + 1);
// Apply the Rendering Equation here.
return emittance + (BRDF * reflected);
}
All these samples must then be averaged to obtain the output color. Note this method of always sampling a random ray in the normal's hemisphere only works well for perfectly diffuse surfaces. For other materials, one generally has to use importance-sampling, i.e. probabilistically select a new ray according to the BRDF's distribution. For instance, a perfectly specular (mirror) material would not work with the method above, as the probability of the new ray being the correct reflected ray – which is the only ray through which any radiance will be reflected – is zero. In these situations, one must divide the reflectance by the probability density function of the sampling scheme, as per Monte-Carlo integration (in the naive case above, there is no particular sampling scheme, so the PDF turns out to be 1).
There are other considerations to take into account to ensure conservation of energy. In particular, in the naive case, the reflectance of a diffuse BRDF must not exceed or the object will reflect more light than it receives (this however depends on the sampling scheme used, and can be difficult to get right).
Bidirectional path tracing
Sampling the integral for a point can be done by either of the following two distinct approaches:
- Shooting rays from the light sources and creating paths in the scene. The path is cut off at a random number of bouncing steps and the resulting light is sent through the projected pixel on the output image. During rendering, billions of paths are created, and the output image is the mean of every pixel that received some contribution.
- Gathering rays from a point on a surface. A ray is projected from the surface to the scene in a bouncing path that terminates when a light source is intersected. The light is then sent backwards through the path and to the output pixel. The creation of a single path is called a "sample". For a single point on a surface, approximately 800 samples (up to as many as 3 thousand samples) are taken. The final output of the pixel is the arithmetic mean of all those samples, not the sum.
Bidirectional Path Tracing combines both Shooting and Gathering in the same algorithm to obtain faster convergence of the integral. A shooting path and a gathering path are traced independently, and then the head of the shooting path is connected to the tail of the gathering path. The light is then attenuated at every bounce and back out into the pixel. This technique at first seems paradoxically slower, since for every gathering sample we additionally trace a whole shooting path. In practice however, the extra speed of convergence far outweighs any performance loss from the extra ray casts on the shooting side.
Performance

A path tracer continuously samples pixels of an image. The image starts to become recognisable after only a few samples per pixel, perhaps 100. However, for the image to "converge" and reduce noise to acceptable levels usually takes around 5000 samples for most images, and many more for pathological cases. Noise is particularly a problem for animations, giving them a normally-unwanted "film-grain" quality of random speckling.
The central performance bottleneck in Path Tracing is the complex geometrical calculation of casting a ray. Importance Sampling is a technique which is motivated to cast fewer rays through the scene while still converging correctly to outgoing luminance on the surface point. This is done by casting more rays in directions in which the luminance would have been greater anyway. If the density of rays cast in certain directions matches the strength of contributions in those directions, the result is identical, but far fewer rays were actually cast. Importance Sampling is used to match ray density to Lambert's Cosine law, and also used to match BRDFs.
Metropolis light transport can result in a lower-noise image with fewer samples. This algorithm was created in order to get faster convergence in scenes in which the light must pass through odd corridors or small holes in order to reach the part of the scene that the camera is viewing. It has also shown promise in correctly rendering pathological situations with caustics. Instead of generating random paths, new sampling paths are created as slight mutations of existing ones. In this sense, the algorithm "remembers" the successful paths from light sources to the camera.
Scattering distribution functions
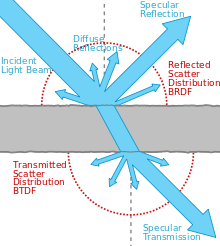
The reflective properties (amount, direction and colour) of surfaces are modelled using BRDFs. The equivalent for transmitted light (light that goes through the object) are BSDFs. A path tracer can take full advantage of complex, carefully modelled or measured distribution functions, which controls the appearance ("material", "texture" or "shading" in computer graphics terms) of an object.
See also
- Arnold (software)
- Blender (software) – 3D modeler that integrates Cycles, a path tracing GPU accelerated rendering engine
- FurryBall Render (GPU)
- Octane Render
Notes
- ^ Kajiya, J. T. (1986). "The rendering equation". Proceedings of the 13th annual conference on Computer graphics and interactive techniques. ACM. CiteSeerX 10.1.1.63.1402
 .
. - ^ Lafortune, E, Mathematical Models and Monte Carlo Algorithms for Physically Based Rendering, (PhD thesis), 1996.
- ^ Purcell, T J; Buck, I; Mark, W; and Hanrahan, P, "Ray Tracing on Programmable Graphics Hardware", Proc. SIGGRAPH 2002, 703 – 712. See also Purcell, T, Ray tracing on a stream processor (PhD thesis), 2004.
- ^ Robison, Austin, "Interactive Ray Tracing on the GPU and NVIRT Overview", slide 37, I3D 2009.
- ^ Vray demo; Other examples include Octane Render, Arion, and Luxrender.
- ^ Veach, E., and Guibas, L. J. Metropolis light transport. In SIGGRAPH’97 (August 1997), pp. 65–76.
- This "Introduction to Global Illumination" has some good example images, demonstrating the image noise, caustics and indirect lighting properties of images rendered with path tracing methods. It also discusses possible performance improvements in some detail.
- SmallPt is an educational path tracer by Kevin Beason. It uses 99 lines of C++ (including scene description). This page has a good set of examples of noise resulting from this technique.