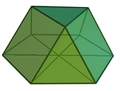
Near-miss Johnson solid
In geometry, a near-miss Johnson solid is a strictly convex polyhedron in which the faces are close to being regular polygons but in which some or all of the faces are not precisely regular. They generalize the Johnson solids, polyhedra in which all faces are regular, and "can often be physically constructed without noticing the discrepancy" between their regular and irregular faces.[1] The precise number of near misses depends on how closely the faces of such a polyhedron are required to approximate regular polygons.
Examples
| Name Conway name |
Image | Vertex configurations |
V | E | F | F3 | F4 | F5 | F6 | F8 | F10 | F12 | Symmetry |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Truncated triangular bipyramid t4dP3[2] |
 |
3 (5.5.5) 12 (4.5.5) |
14 | 21 | 9 | 3 | 6 | Dih3 | |||||
| Truncated triakis tetrahedron t6kT[3] |
 |
4 (5.5.5) 24 (5.5.6) |
28 | 42 | 16 | 12 | 4 | Td, [3,3] order 24 | |||||
| Chamfered cube cC[4] |
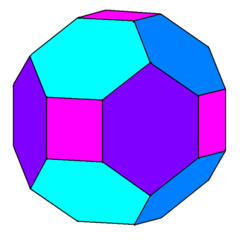 |
24 (4.6.6) 8 (6.6.6) |
32 | 48 | 18 | 6 | 12 | Oh, [4,3] order 48 | |||||
| -- | 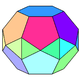 |
12 (5.5.6) 6 (3.5.3.5) 12 (3.3.5.5) |
30 | 54 | 26 | 12 | 12 | 2 | D6h, [6,2] order 24 | ||||
| -- |  |
6 (5.5.5) 9 (3.5.3.5) 12 (3.3.5.5) |
27 | 51 | 26 | 14 | 12 | D3h, [3,2] order 12 | |||||
| Tetrated dodecahedron |  |
4 (5.5.5) 12 (3.5.3.5) 12 (3.3.5.5) |
28 | 54 | 28 | 16 | 12 | Td, [3,3] order 24 | |||||
| Chamfered dodecahedron cD[5] |
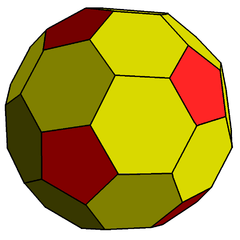 |
60 (5.6.6) 20 (6.6.6) |
80 | 120 | 42 | 12 | 30 | Ih, [5,3] order 120 | |||||
| Rectified truncated icosahedron atI[6] |
 |
60 (3.5.3.6) 30 (3.6.3.6) |
90 | 180 | 92 | 60 | 12 | 20 | Ih, [5,3] order 120 | ||||
| Truncated truncated icosahedron ttI[7] |
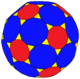 |
120 (3.10.12) 60 (3.12.12) |
180 | 270 | 92 | 60 | 12 | 20 | Ih, [5,3] order 120 | ||||
| Expanded truncated icosahedron etI[8] |
 |
60 (3.4.5.4) 120 (3.4.6.4) |
180 | 360 | 182 | 60 | 90 | 12 | 20 | Ih, [5,3] order 120 | |||
| Snub rectified truncated icosahedron stI[9] |
 |
60 (3.3.3.3.5) 120 (3.3.3.3.6) |
180 | 450 | 272 | 240 | 12 | 20 | I, [5,3]+ order 60 |
Coplanar misses
Some failed Johnson solid candidates have coplanar faces. These polyhedra can be perturbed to become convex with faces that are arbitrarily close to regular polygons. These cases use 4.4.4.4 vertex figures of the square tiling, 3.3.3.3.3.3 vertex figure of the triangular tiling, as well as 60 degree rhombi divided double equilateral triangle faces, or a 60 degree trapezoid as three equilateral triangles.
Examples: 3.3.3.3.3.3
-

Rhombic prism
-
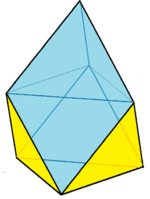
Gyroelongated trigonal pyramid
-
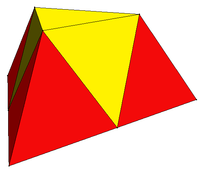
Triangulated monorectified tetrahedron
-
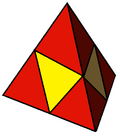
Tetratetrahedron, Triangulated tetrahedron
-

Augmented triangular cupola
-

Triangulated truncated triangular bipyramid
4.4.4.4
3.4.6.4:
-
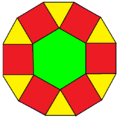
Hexagonal cupola
(Degenerate)
See also
References
- ↑ Kaplan, Craig S.; Hart, George W. (2001), "Symmetrohedra: Polyhedra from Symmetric Placement of Regular Polygons", Bridges: Mathematical Connections in Art, Music and Science (PDF).
- ↑ http://levskaya.github.io/polyhedronisme/?recipe=C100A1t4dP3
- ↑ http://levskaya.github.io/polyhedronisme/?recipe=C100A1t6kT
- ↑ http://levskaya.github.io/polyhedronisme/?recipe=C100A1cC
- ↑ http://levskaya.github.io/polyhedronisme/?recipe=C100A1cD
- ↑ http://levskaya.github.io/polyhedronisme/?recipe=C400A1atI
- ↑ http://levskaya.github.io/polyhedronisme/?recipe=C1000ttI
- ↑ http://levskaya.github.io/polyhedronisme/?recipe=C1000aatI
- ↑ http://levskaya.github.io/polyhedronisme/?recipe=C1000stI