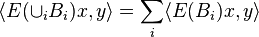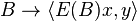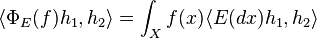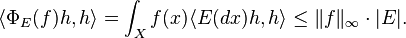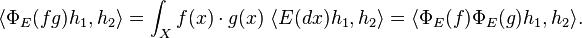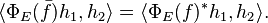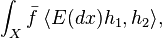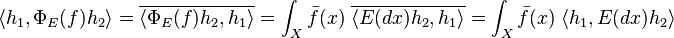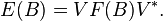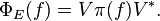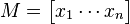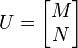Naimark's dilation theorem

In operator theory, Naimark's dilation theorem is a result that characterizes positive operator valued measures. It can be viewed as a consequence of Stinespring's dilation theorem.

Note

In the mathematical literature, one may also find other results that bear Naimark's name.

Spelling

In the physics literature, it is common to see the spelling "Neumark" instead of "Naimark." This is due to translating between the Russian alphabet spelling and the spelling in European languages (namely English and German) using the Roman alphabet.

Some preliminary notions

Let X be a compact Hausdorff space, H be a Hilbert space, and L(H) the Banach space of bounded operators on H. A mapping E from the Borel σ-algebra on X to 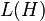$L(H)$ is called a operator-valued measure if it is weakly countably additive, that is, for any disjoint sequence of Borel sets 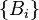$\{ B_i \}$ , we have

\langle E (\cup _i B_i) x, y \rangle = \sum_i \langle E (B_i) x, y \rangle

for all x and y. Some terminology for describing such measures are:

E is called regular if the scalar valued measure

B \rightarrow \langle E (B) x, y \rangle

is a regular Borel measure, meaning all compact sets have finite total variation and the measure of a set can be approximated by those of open sets.

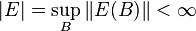E is called bounded if $|E| = \sup_B \|E(B) \| < \infty$ .
E is called positive if E(B) is a positive operator for all B.
E is called self-adjoint if E(B) is self-adjoint for all B.
E is called spectral if it is self-adjoint and 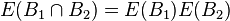$E (B_1 \cap B_2) = E(B_1) E(B_2)$ for all $B_1, B_2$ .

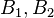We will assume throughout that E is regular.

Let C(X) denote the abelian C*-algebra of continuous functions on X. If E is regular and bounded, it induces a map 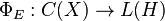$\Phi _E : C(X) \rightarrow L(H)$ in the obvious way:

\langle \Phi _E (f) h_1 , h_2 \rangle = \int _X f(x) \langle E(dx) h_1, h_2 \rangle

The boundedness of E implies, for all h of unit norm

\langle \Phi _E (f) h , h \rangle = \int _X f(x) \langle E(dx) h, h \rangle \leq \| f \|_\infty \cdot |E| .

This shows 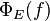$\; \Phi _E (f)$ is a bounded operator for all f, and 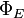$\Phi _E$ itself is a bounded linear map as well.

The properties of 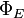$\Phi_E$ are directly related to those of E:

If E is positive, then 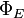$\Phi_E$ , viewed as a map between C*-algebras, is also positive.
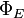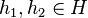$\Phi_E$ is a homomorphism if, by definition, for all continuous f on X and $h_1, h_2 \in H$ ,

\langle \Phi_E (fg) h_1, h_2 \rangle = \int _X f(x) \cdot g(x) \; \langle E(dx) h_1, h_2 \rangle = \langle \Phi_E (f) \Phi_E (g) h_1 , h_2 \rangle.

Take f and g to be indicator functions of Borel sets and we see that 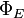$\Phi _E$ is a homomorphism if and only if E is spectral.

Similarly, to say 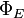$\Phi_E$ respects the * operation means

\langle \Phi_E ( {\bar f} ) h_1, h_2 \rangle = \langle \Phi_E (f) ^* h_1 , h_2 \rangle.

The LHS is

\int _X {\bar f} \; \langle E(dx) h_1, h_2 \rangle,

and the RHS is

\langle h_1, \Phi_E (f) h_2 \rangle = \overline{\langle \Phi_E(f) h_2, h_1 \rangle} = \int _X {\bar f}(x) \; \overline{\langle E(dx) h_2, h_1 \rangle} = \int _X {\bar f}(x) \; \langle h_1, E(dx) h_2 \rangle

So, taking f a sequence of continuous functions increasing to the indicator function of B, we get 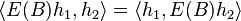$\langle E(B) h_1, h_2 \rangle = \langle h_1, E(B) h_2 \rangle$ , i.e. E(B) is self adjoint.

Combining the previous two facts gives the conclusion that 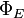$\Phi _E$ is a *-homomorphism if and only if E is spectral and self adjoint. (When E is spectral and self adjoint, E is said to be a projection-valued measure or PVM.)

Naimark's theorem

The theorem reads as follows: Let E be a positive L(H)-valued measure on X. There exists a Hilbert space K, a bounded operator 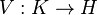$V: K \rightarrow H$ , and a self-adjoint, spectral L(K)-valued measure on X, F, such that

\; E(B) = V F(B) V^*.

Proof

We now sketch the proof. The argument passes E to the induced map 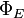$\Phi_E$ and uses Stinespring's dilation theorem. Since E is positive, so is 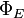$\Phi_E$ as a map between C*-algebras, as explained above. Furthermore, because the domain of 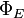$\Phi _E$ , C(X), is an abelian C*-algebra, we have that 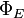$\Phi_E$ is completely positive. By Stinespring's result, there exists a Hilbert space K, a *-homomorphism 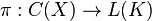$\pi : C(X) \rightarrow L(K)$ , and operator 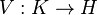$V: K \rightarrow H$ such that

\; \Phi_E(f) = V \pi (f) V^*.

Since π is a *-homomorphism, its corresponding operator-valued measure F is spectral and self adjoint. It is easily seen that F has the desired properties.

Finite-dimensional case

In the finite-dimensional case, there is a somewhat more explicit formulation.

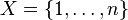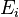Suppose now $X = \{1, \dotsc, n \}$ , therefore C(X) is the finite-dimensional algebra $\mathbb{C}^n$ , and H has finite dimension m. A positive operator-valued measure E then assigns each i a positive semidefinite m × m matrix $E_i$ . Naimark's theorem now states that there is a projection-valued measure on X whose restriction is E.

Of particular interest is the special case when 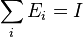$\sum_i E_i = I$ where I is the identity operator. (See the article on POVM for relevant applications.) In this case, the induced map 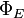$\Phi_E$ is unital. It can be assumed with no loss of generality that each 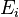$E_i$ is a rank-one projection onto some 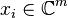$x_i \in \mathbb{C}^m$ . Under such assumptions, the case 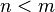$n < m$ is excluded and we must have either

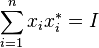$n = m$ and E is already a projection-valued measure (because $\sum_{i=1}^n x_i x_i^* = I$ if and only if $\{x_i\}$ is an orthonormal basis),
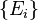$n > m$ and $\{ E_i \}$ does not consist of mutually orthogonal projections.

For the second possibility, the problem of finding a suitable projection-valued measure now becomes the following problem. By assumption, the non-square matrix

M = \begin{bmatrix} x_1 \cdots x_n \end{bmatrix}

is an isometry, that is 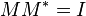$M M^* = I$ . If we can find a 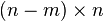$(n-m) \times n$ matrix N where

U = \begin{bmatrix} M \\ N \end{bmatrix}

is a n × n unitary matrix, the projection-valued measure whose elements are projections onto the column vectors of U will then have the desired properties. In principle, such a N can always be found.

References

V. Paulsen, Completely Bounded Maps and Operator Algebras, Cambridge University Press, 2003.

This article is issued from Wikipedia - version of the 3/22/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.