Multiple-conclusion logic

A multiple-conclusion logic is one in which logical consequence is a relation, 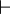$\vdash$ , between two sets of sentences (or propositions). 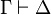$\Gamma \vdash \Delta$ is typically interpreted as meaning that whenever each element of 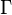$\Gamma$ is true, some element of 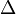$\Delta$ is true; and whenever each element of 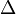$\Delta$ is false, some element of 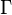$\Gamma$ is false.

This form of logic was developed in the 1970s by D. J. Shoesmith and Timothy Smiley^[1] but has not been widely adopted.

Some logicians favor a multiple-conclusion consequence relation over the more traditional single-conclusion relation on the grounds that the latter is asymmetric (in the informal, non-mathematical sense) and favors truth over falsity (or assertion over denial).

References

↑ D. J. Shoesmith and T. J. Smiley, Multiple Conclusion Logic, Cambridge University Press, 1978

This article is issued from Wikipedia - version of the 12/30/2010. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Multiple-conclusion logic

See also

References