Mean Directional Accuracy (MDA)

Mean Directional Accuracy (MDA), also known as Mean Direction Accuracy, is a measure of prediction accuracy of a forecasting method in statistics. It compares the forecast direction (upward or downward) to the actual realized direction. It is defined by the following formula

\frac{1}{N}\sum_t \mathbf{1}_{sign(A_t - A_{t-1}) == sign(F_t - F_{t-1})}

where At is the actual value at time t and Ft is the forecast value at time t. Variable N represents number of forecasting points. The function 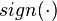sign(\cdot) is sign function and \mathbf{1} is the indicator function.

In simple words, MDA provides the probability that the under study forecasting method can detect the correct direction of the time series. MDA is a popular metric for forecasting performance in economics and finance.[1][2]

MDA is used in economics applications where the economists is often interested only in directional movement of variable of interest. As an example in macroeconomics, a monetary authority who likes to know the direction of the inflation, to raises interest rates or decrease the rates if inflation is predicted to rise or drop respectively.[3] Another example can be found in financial planning where the user wants to know if the demand has increasing direction or decreasing trend.[4]

Comparison to Other Forecasting Metrics

Many techniques such as Mean absolute percentage error or Median absolute deviation evaluate forecasting and provided information about the accuracy and value of the forecasts. While accuracy, as measured by quantitative errors, is important, it may be more crucial to accurately forecast the direction of change. Directional accuracy is similar to a binary evaluation. The metric only consider the upward or downward direction in the time series and is independent of quantitive value of increase or decrease. For example, Will prices rise or fall? How much it will increase or decrease can be detected by other forecasting metrics.[5]

References

  1. ↑ Pesaran, M. H., & Timmermann, A. (2004). How costly is it to ignore breaks when forecasting the direction of a time series?. International Journal of Forecasting, 20(3), 411-425
  2. ↑ Schnader, M. H., & Stekler, H. O. (1990). Evaluating predictions of change. Journal of Business, 99-107
  3. ↑ Greer, M. (2003). Directional accuracy tests of long-term interest rate forecasts. International Journal of Forecasting, 19(2), 291-298.
  4. ↑ Blaskowitz, O., & Herwartz, H. (2011). On economic evaluation of directional forecasts. International Journal of Forecasting, 27(4), 1058-1065.
  5. ↑ Sinclair, T. M., Stekler, H. O., & Kitzinger, L. (2010). Directional forecasts of GDP and inflation: a joint evaluation with an application to Federal Reserve predictions. Applied Economics, 42(18), 2289-2297.
This article is issued from Wikipedia - version of the 1/30/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.