Marching squares
Marching squares is a computer graphics algorithm that generates contours for a two-dimensional scalar field (rectangular array of individual numerical values). A similar method can be used to contour 2D triangle meshes.
The contours can be of two kinds:
- Isolines - lines following a single data level, or isovalue.
- Isobands - filled areas between isolines.
Typical applications include the Contour lines on topographic maps or the generation of isobars for weather maps.
Marching squares takes a similar approach to the 3D marching cubes algorithm:
- Process each cell in the grid independently.
- Calculate a cell index using comparisons of the contour level(s) with the data values at the cell corners.
- Use a pre-built lookup table, keyed on the cell index, to describe the output geometry for the cell.
- Apply linear interpolation along the boundaries of the cell to calculate the exact contour position.
Isoline
Basic algorithm
Here are the steps of the algorithm:
Apply a threshold to the 2D field to make a binary image containing:
- 1 where the data value is above the isovalue
- 0 where the data value is below the isovalue
Every 2x2 block of pixels in the binary image forms a contouring cell, so the whole image is represented by a grid of such cells (shown in green in the picture below). Note that this contouring grid is one cell smaller in each direction than the original 2D field.
For each cell in the contouring grid:
- Compose the 4 bits at the corners of the cell to build a binary index: walk around the cell in a clockwise direction appending the bit to the index, using bitwise OR and left-shift, from most significant bit at the top left, to least significant bit at the bottom left. The resulting 4-bit index can have 16 possible values in the range 0-15.
- Use the cell index to access a pre-built lookup table with 16 entries listing the edges needed to represent the cell (shown in the lower right part of the picture below).
- Apply linear interpolation between the original field data values to find the exact position of the contour line along the edges of the cell.

Disambiguation of saddle points
The contour is ambiguous at saddle points. It is possible to resolve the ambiguity by using the average data value for the center of the cell to choose between different connections of the interpolated points. Here is another summary of the method showing options for the saddle:
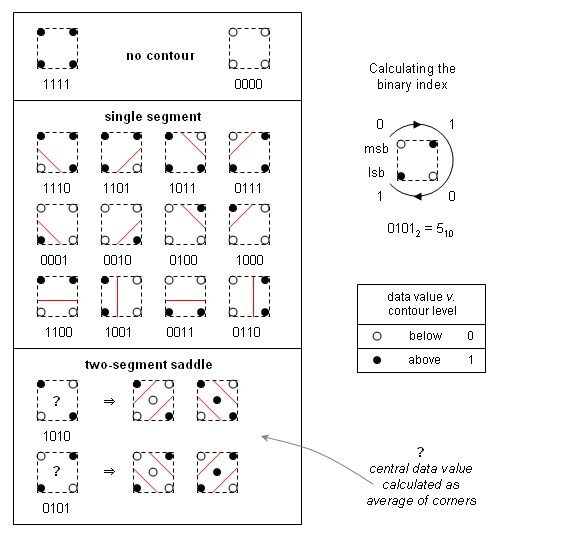
The central value is used to flip the index value before looking-up the cell geometry in the table, i.e. if the index is 0101=5 and the central value is below, then lookup index 10; similarly, if the index is 1010=10 and the central value is above, then lookup index 5.
Isoband
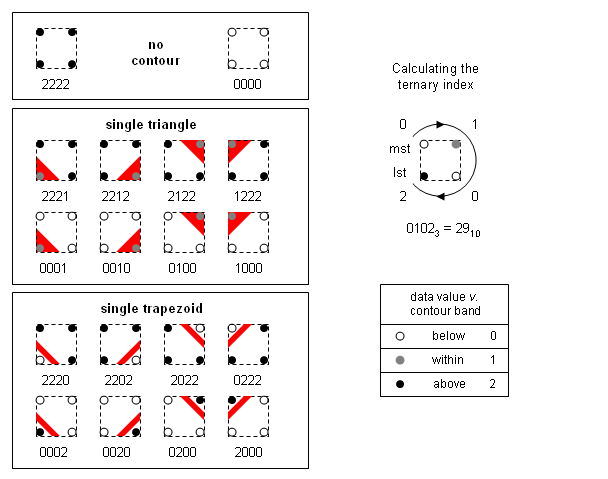
A similar algorithm can be created for filled contour bands within upper and lower threshold values. To build the index we compare the data values at the cell corners with the two contour threshold values. There are now 3 possibilities:
- 0 - corner data value below lower band level
- 1 - corner data value within band interval
- 2 - corner data value above upper level
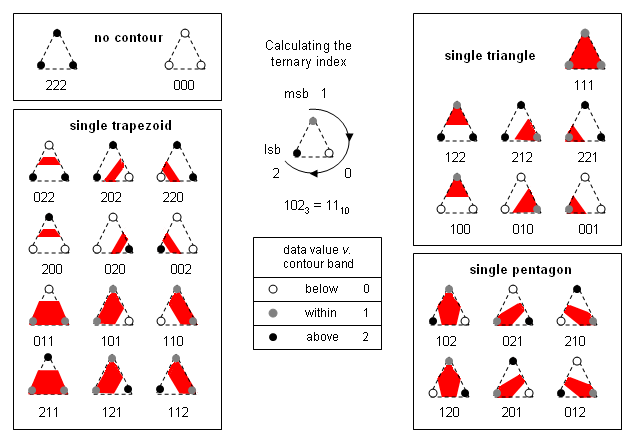
The index will be ternary value built from these ternary digits, or trits. We build the index as before, by walking clockwise around the cell, appending each trit to the index, taking the most-significant-trit from the top left corner, and the least-significant-trit from the bottom left corner. There will now be 81 possibilities, rather than 16 for isolines.
Each cell will be filled with 0, 1 or 2 polygonal fragments, each with 3-8 sides. The action for each cell is based on the category of the ternary index:
- Empty - no fragments for index values 0 (0000) or 80 (2222).
- Not Empty - walk around the cell adding corner positions that are within the band and interpolating along relevant edges; use the index to decide how to connect the list of points:
- Slope - build a single polygon fragment with 3-7 sides.
- Saddle - calculate the average value to help disambiguation; then use the index and the central value to build 1 or 2 polygonal fragments with a total of 6, 7 or 8 sides.
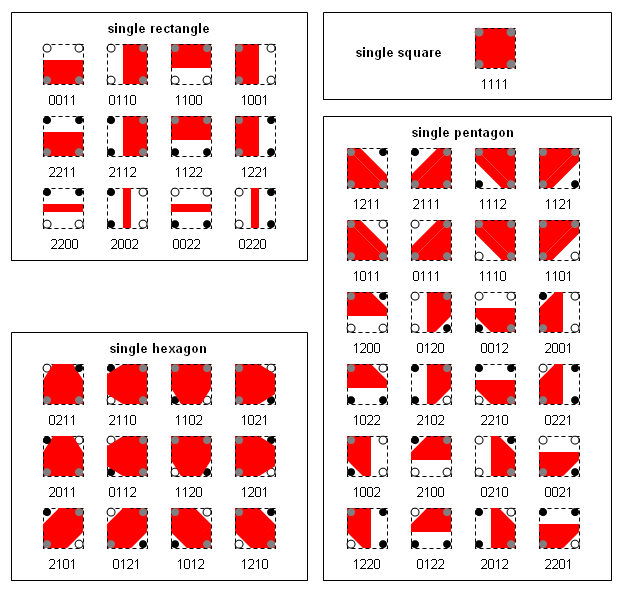

The case missing from the 6-sided saddles is for a central value that cannot occur.
There is a valid case omitted from each 7-sided saddle, where the central value is dominated by a single extreme value. The resulting geometric structure would be too complex to fit the simple model of two convex fragments, so it is merged with the case where the central value is within the band. The linear interpolation in such cases will produce a plausible single heptagon.
Meandering triangles
The same basic algorithm can be applied to triangular meshes, which consist of connected triangles with data assigned to the vertices. For example, a scattered set of data points could be connected with a Delaunay triangulation to allow the data field to be contoured. A triangular cell is always planar, because it is a 2-simplex (i.e. specified by n+1 vertices in an n-dimensional space). There is always a unique linear interpolant across a triangle and no possibility of an ambiguous saddle.
The analysis for isolines over triangles is especially simple: there are 3 binary digits, so 8 possibilities:
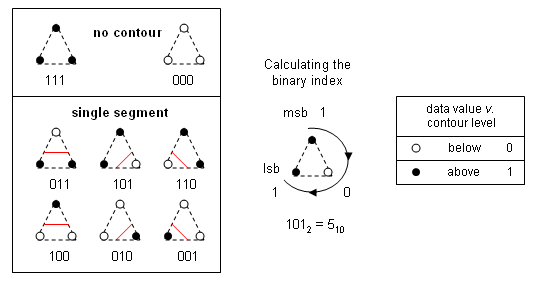
The analysis for isobands over triangles requires 3 ternary trits, so 27 possibilities:
Dimensions and spaces
The data space for the Marching Squares algorithm is 2D, because the vertices assigned a data value are connected to their neighbors in a 2D topological grid, but the spatial coordinates assigned to the vertices can be in 2D, 3D or higher dimensions.
For example, a triangular mesh may represent a 2D data surface embedded in 3D space, where spatial positions of the vertices and interpolated points along a contour will all have 3 coordinates. Note that the case of squares is ambiguous again, because a quadrilateral embedded in 3-dimensional space is not necessarily planar, so there is a choice of geometrical interpolation scheme to draw the banded surfaces in 3D.
Performance considerations
The algorithm is embarrassingly parallel, because all cells are processed independently. It is easy to write a parallel algorithm assuming:
- Shared read-only input scalar field.
- Shared append-only geometry output stream.
A naive implementation of Marching Squares that processes every cell independently will perform every linear interpolation twice (isoline) or four times (isoband). Similarly, the output will contain 2 copies of the 2D vertices for disjoint lines (isoline) or 4 copies for polygons (isobands). [Under the assumptions that: the grid is large, so that most cells are internal; and a full contiguous set of isobands is being created.]
It is possible to reduce the computational overhead by caching the results of interpolation. For example, a single-threaded serial version would only need to cache interpolated results for one row of the input grid.
It is also possible to reduce the size of the output by using indexed geometric primitives, i.e. create an array of 2D vertices and specify lines or polygons with short integer offsets into the array.
References
- Maple, C. (2003). "Geometric design and space planning using the marching squares and marching cube algorithms". Proc. 2003 Intl. Conf. Geometric Modeling and Graphics: 90–95. doi:10.1109/GMAG.2003.1219671.
- Banks, D. C. (2004). "Counting cases in substitope algorithms". IEEE Trans. Visual. Comp. Graphics. 10 (4): 371–384. doi:10.1109/TVCG.2004.6.
- Laguardia, J. J.; Cueto, E.; Doblaré, M. (2005). "A natural neighbour Galerkin method with quadtree structure". Int. J. Numer. Meth. Engineer. 63 (6): 789–812. doi:10.1002/nme.1297.
- Schaefer, Scott; Warren, Joe (2005). "Dual marching cubes: prima contouring and dual grids". Comp. Graph. forum. 24 (2): 195–201. doi:10.111/j.1467-8659.2005.00843.x.
- Mantz, Huber; Jacobs, Karin; Mecke, Klaus (2008). "Utilizing Minkowski functionals for image analysis: a marching square algorithm". J. Stat. Mech. Theory Exper. (12): P12015. doi:10.1088/1742-5468/2008/12/P12015.
- Cipolletti, Marina P.; Delrieux, Claudio A.; Perillo, Gerardo M. E.; Piccolo, M. Cintia (2012). "Superresolution border segmentation and measurement in remote sensing images". Comp. Geosci. 40: 87–97. doi:10.1016/j.cageo.2011.07.015.
External links
- Marching Square Matlab algorithm - An easy to understand open-source marching square algorithm.
- Isoline Isoband - Algorithm descriptions and open source C/Fortran code for the AVS scientific visualization system (Mike French, 1992).
- implementation in Java
- Marching Squares code in Java. Given a 2D data set and thresholds, returns GeneralPath[] for easy plotting.