Lusternik–Schnirelmann category

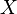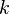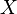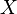In mathematics, the Lyusternik–Schnirelmann category (or, Lusternik–Schnirelmann category, LS-category) of a topological space $X$ is the homotopical invariant defined to be the smallest integer number $k$ such that there is an open covering $\{U_i\}_{1\leq i\leq k}$ of $X$ with the property that each inclusion map $U_i\hookrightarrow X$ is nullhomotopic. For example, if $X$ is a sphere, this takes the value two.

Sometimes a different normalization of the invariant is adopted, which is one less than the definition above Such a normalization has been adopted in the definitive monograph by Cornea, Lupton, Oprea, and Tanré (see below).

In general it is not easy to compute this invariant, which was initially introduced by Lazar Lyusternik and Lev Schnirelmann in connection with variational problems. It has a close connection with algebraic topology, in particular cup-length. In the modern normalization, the cup-length is a lower bound for LS category.

It was, as originally defined for the case of X a manifold, the lower bound for the number of critical points that a real-valued function on X could possess (this should be compared with the result in Morse theory that shows that the sum of the Betti numbers is a lower bound for the number of critical points of a Morse function).

The invariant has been generalized in several different directions (group actions, foliations, simplicial complexes,...)

References

R. H. Fox, On the Lusternik-Schnirelmann category, Annals of Mathematics 42 (1941), 333–370.
F. Takens, The minimal number of critical points of a function on compact manifolds and the Lusternik-Schnirelmann category, Inventiones Mathematicae 6 (1968), 197–244.
Tudor Ganea, Some problems on numerical homotopy invariants, Lecture Notes in Math. 249 (Springer, Berlin, 1971), pp. 13 – 22 MR 0339147
Ioan James, On category, in the sense of Lusternik-Schnirelmann, Topology 17 (1978), 331–348.
Clapp, Mónica; Puppe, Dieter Invariants of the Lusternik-Schnirelmann type and the topology of critical sets. Trans. Amer. Math. Soc. 298 (1986), no. 2, 603–620.
Octav Cornea, Gregory Lupton, John Oprea, Daniel Tanré, Lusternik-Schnirelmann category, Mathematical Surveys and Monographs, 103. American Mathematical Society, Providence, RI, 2003 ISBN 0-8218-3404-5

This article is issued from Wikipedia - version of the 5/19/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Lusternik–Schnirelmann category

See also

References