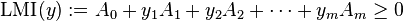Linear matrix inequality
In convex optimization, a linear matrix inequality (LMI) is an expression of the form
where
-
![y=[y_i\,,~i\!=\!1,\dots, m]](../I/m/1ed1f534a4c0a56a07dad7a654f02a02.png) is a real vector,
is a real vector, -
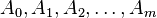 are
are 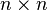 symmetric matrices
symmetric matrices 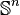 ,
, -
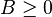 is a generalized inequality meaning
is a generalized inequality meaning 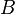 is a positive semidefinite matrix belonging to the positive semidefinite cone
is a positive semidefinite matrix belonging to the positive semidefinite cone 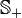 in the subspace of symmetric matrices
in the subspace of symmetric matrices 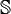 .
.
This linear matrix inequality specifies a convex constraint on y.
Applications
There are efficient numerical methods to determine whether an LMI is feasible (e.g., whether there exists a vector y such that LMI(y) ≥ 0), or to solve a convex optimization problem with LMI constraints. Many optimization problems in control theory, system identification and signal processing can be formulated using LMIs. Also LMIs find application in Polynomial Sum-Of-Squares. The prototypical primal and dual semidefinite program is a minimization of a real linear function respectively subject to the primal and dual convex cones governing this LMI.
Solving LMIs
A major breakthrough in convex optimization lies in the introduction of interior-point methods. These methods were developed in a series of papers and became of true interest in the context of LMI problems in the work of Yurii Nesterov and Arkadii Nemirovskii.
References
- Y. Nesterov and A. Nemirovsky, Interior Point Polynomial Methods in Convex Programming. SIAM, 1994.
External links
- S. Boyd, L. El Ghaoui, E. Feron, and V. Balakrishnan, Linear Matrix Inequalities in System and Control Theory (book in pdf)
- C. Scherer and S. Weiland Course on Linear Matrix Inequalities in Control, Dutch Institute of Systems and Control (DISC).