Leray's theorem
In algebraic geometry, Leray's theorem relates abstract sheaf cohomology with Čech cohomology.
Let  be a sheaf on a topological space
be a sheaf on a topological space 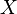 and
and  an open cover of
an open cover of  If
If  is acyclic on every finite intersection of elements of
is acyclic on every finite intersection of elements of  , then
, then
where  is the
is the 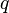 -th Čech cohomology group of
-th Čech cohomology group of  with respect to the open cover
with respect to the open cover 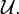
References
- Bonavero, Laurent. Cohomology of Line Bundles on Toric Varieties, Vanishing Theorems. Lectures 16-17 from "Summer School 2000: Geometry of Toric Varieties."
This article incorporates material from Leray's theorem on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
This article is issued from Wikipedia - version of the 2/17/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.