Leaf area index

Leaf area index (LAI) is a dimensionless quantity that characterizes plant canopies. It is defined as the one-sided green leaf area per unit ground surface area (LAI = leaf area / ground area, m2 / m2) in broadleaf canopies.[1] In conifers, three definitions for LAI have been used:

LAI ranges from 0 (bare ground) to over 10 (dense conifer forests).

Interpretation and application of LAI

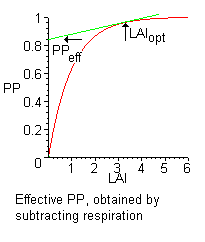
LAI is used to predict photosynthetic primary production, evapotranspiration and as a reference tool for crop growth. As such, LAI plays an essential role in theoretical production ecology. An inverse exponential relation between LAI and light interception, which is linearly proportional to the primary production rate, has been established:

where Pmax designates the maximum primary production and designates a crop-specific growth coefficient. This inverse exponential function is called the primary production function.

Determining LAI

LAI can be determined directly by taking a statistically significant sample of foliage from a plant canopy, measuring the leaf area per sample plot and dividing it by the plot land surface area. Indirect methods measure canopy geometry or light extinction and relate it to LAI.[3]

Direct methods

Direct methods can be easily applied on deciduous species by collecting leaves during leaf fall in traps of certain area distributed below the canopy. The area of the collected leaves can be measured using a leaf area meter or an image scanner and image analysis software. The measured leaf area can then be divided by the area of the traps to obtain LAI. Alternatively, leaf area can be measured on a sub-sample of the collected leaves and linked to the leaf dry mass (e.g. via Specific Leaf Area, SLA cm2/g). That way it is not necessary to measure the area of all leaves one by one, but weigh the collected leaves after drying (at 60–80 °C for 48 h). Leaf dry mass multiplied by the specific leaf area is converted into leaf area.
Direct methods in evergreen species are necessarily destructive. However, they are widely used in crops and pastures by harvesting the vegetation and measuring leaf area within a certain ground surface area. It is very difficult (and also unethical) to apply such destructive techniques in natural ecosystems, particularly in forests of evergreen tree species. Foresters have developed techniques that determine leaf area in evergreen forests through allometric relationships.
Due to the difficulties and the limitations of the direct methods for estimating LAI, they are mostly used as reference for indirect methods that are easier and faster to apply.

Indirect methods

A hemispherical photograph of forest canopy. The ratio of the area of canopy to sky is used to approximate LAI.

Indirect methods of estimating LAI in situ can be divided in two categories:

  1. indirect contact LAI measurements such as plumb lines and inclined point quadrats
  2. indirect non-contact measurements

Due to the subjectivity and labor involved with the first method, indirect non-contact measurements are typically preferred. Non-contact LAI tools, such as hemispherical photography, Hemiview Plant Canopy Analyser from Delta-T Devices, the CI-110 Plant Canopy Analyzer from CID Bio-Science, LAI-2200 Plant Canopy Analyzer from LI-COR Biosciences and the LP-80 LAI ceptometer from Decagon Devices, measure LAI in a non-destructive way. Hemispherical photography methods estimate LAI and other canopy structure attributes from analyzing upward-looking fisheye photographs taken beneath the plant canopy. The LAI-2200 calculates LAI and other canopy structure attributes from solar radiation measurements made with a wide-angle optical sensor. Measurements made above and below the canopy are used to determine canopy light interception at five angles, from which LAI is computed using a model of radiative transfer in vegetative canopies. The LP-80 calculates LAI by means of measuring the difference between light levels above the canopy and at ground level, and factoring in the leaf angle distribution, solar zenith angle, and plant extinction coefficient. Such indirect methods, where LAI is calculated based upon observations of other variables (canopy geometry, light interception, leaf length and width,[4] etc.) are generally faster, amenable to automation, and thereby allow for a larger number of spatial samples to be obtained. For reasons of convenience when compared to the direct (destructive) methods, these tools are becoming more and more important.

Disadvantages of methods

The disadvantage of the direct method is that it is destructive, time consuming and expensive, especially if the study area is very large.

The disadvantage of the indirect method is that in some cases it can underestimate the value of LAI in very dense canopies, as it does not account for leaves that lie on each other, and essentially act as one leaf according to the theoretical LAI models.[5] Ignorance of non-randomness within canopies may cause underestimation of LAI up to 25%, introducing path length distribution in the indirect method can improve the measuring accuracy of LAI.[6]

See also

Notes

  1. ↑ Watson, D.J., 1947. Comparative physiological studies on the growth of field crops: I. Variation in net assimilation rate and leaf area between species and varieties and within and between years. Annals of Botany, 11: 41-76.
  2. ↑ Chen, J.M., and Black, T.A. (1992): Defining leaf area index for non-flat leaves. Agricultural and Forest Meteorology 57: 1–12
  3. ↑ Breda, N, (2003). Ground-based measurements of leaf area index: A review of methods, instruments and current controversies. Journal of Experimental Botany, 54, 2403–2417
  4. ↑ Blanco, F.F.; Folegatti, M.V. (2003). "A new method for estimating the leaf area index of cucumber and tomato plants". Horticultura Brasileira. 21 (4): 666–669. doi:10.1590/S0102-05362003000400019.
  5. ↑ W.W. Wilhelm, K. Ruwe, M.R. Schlemmer (2000), "Comparisons of three Leaf Area Index Meters in a Corn Canopy” Crop Science 40:1179-1183
  6. ↑ R. Hu, G. Yan*, X. Mu, J. Luo (2014), Indirect measurement of leaf area index on the basis of path length distribution, Remote Sensing of Environment, 155: 239-247.

References

This article is issued from Wikipedia - version of the 6/25/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.