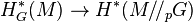Kirwan map

In differential geometry, the Kirwan map, introduced by British mathematician Frances Kirwan, is the homomorphism

H^*_G(M) \to H^*(M /\!/_p G)

where

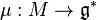M is a Hamiltonian G-space; i.e., a symplectic manifold acted by a Lie group G with a moment map $\mu: M \to {\mathfrak g}^*$ .
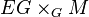$H^*_G(M)$ is the equivariant cohomology ring of M; i.e.. the cohomology ring of the homotopy quotient $EG \times_G M$ of M by G.
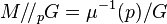$M /\!/_p G = \mu^{-1}(p)/G$ is the symplectic quotient of M by G at a regular central value 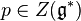$p \in Z({\mathfrak g}^*)$ of $\mu$ .

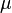It is defined as the map of equivariant cohomology induced by the inclusion 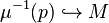$\mu^{-1}(p) \hookrightarrow M$ followed by the canonical isomorphism $H_G^*(\mu^{-1}(p)) = H^*(M /\!/_p G)$ .

A theorem of Kirwan says that if M is compact, then the map is surjective in rational coefficients. The analogous result holds between the K-theory of the symplectic quotient and the equivariant topological K-theory of M.^[1]

References

↑ M. Harada, G. Landweber. Surjectivity for Hamiltonian G-spaces in K-theory. Trans. Amer. Math. Soc. 359 (2007), 6001--6025.

F. C. Kirwan, Cohomology of Quotients in Complex and Algebraic Geometry, Mathematical Notes 31, Princeton University Press, Princeton N. J., 1984.

This article is issued from Wikipedia - version of the 10/28/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.