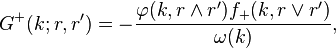Jost function
In scattering theory, the Jost function is the Wronskian of the regular solution and the (irregular) Jost solution to the differential equation  .
It was introduced by Res Jost.
.
It was introduced by Res Jost.
Background
We are looking for solutions 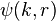 to the radial Schrödinger equation in the case
to the radial Schrödinger equation in the case 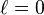 ,
,
Regular and irregular solutions
A regular solution 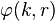 is one that satisfies the boundary conditions,
is one that satisfies the boundary conditions,
If 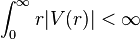 , the solution is given as a Volterra integral equation,
, the solution is given as a Volterra integral equation,
We have two irregular solutions (sometimes called Jost solutions) 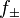 with asymptotic behavior
with asymptotic behavior  as
as 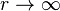 . They are given by the Volterra integral equation,
. They are given by the Volterra integral equation,
If 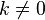 , then
, then 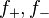 are linearly independent. Since they are solutions to a second order differential equation, every solution (in particular
are linearly independent. Since they are solutions to a second order differential equation, every solution (in particular 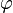 ) can be written as a linear combination of them.
) can be written as a linear combination of them.
Jost function definition
The Jost function is
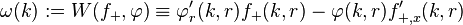 ,
,
where W is the Wronskian. Since 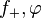 are both solutions to the same differential equation, the Wronskian is independent of r. So evaluating at
are both solutions to the same differential equation, the Wronskian is independent of r. So evaluating at 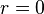 and using the boundary conditions on
and using the boundary conditions on 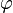 yields
yields 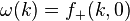 .
.
Applications
The Jost function can be used to construct Green's functions for
In fact,
where 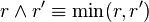 and
and 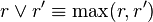 .
.
References
- Roger G. Newton, Scattering Theory of Waves and Particles.
- D. R. Yafaev, Mathematical Scattering Theory.
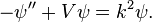
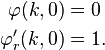
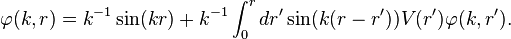
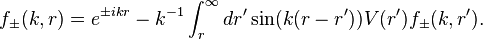
![\left[-\frac{\partial^2}{\partial r^2}+V(r)-k^2\right]G=-\delta(r-r').](../I/m/61f55ff8997e95b8410e83ba6a1ab3e6.png)