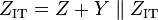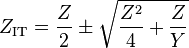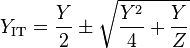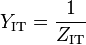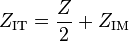Iterative impedance

Iterative impedance is the input impedance of an infinite chain of identical networks. It is related to the image impedance used in filter design, but has a simpler, more straightforward definition.

Definition

Iterative impedance is the input impedance of one port of a two-port network when the other port is connected to an infinite chain of identical networks.[1] Equivalently, iterative impedance is that impedance that when connected to port 2 of a two-port network is equal to the impedance measured at port 1. This can be seen to be equivalent by considering the infinite chain of identical networks connected to port 2 in the first definition. If the original network is removed then port 1 of the second network will present the same iterative impedance as before since port 2 of the second netork still has an infinite chain of networks connected to it. Thus the whole infinite chain can be replaced with a single lumped impedance equal to the iterative impedance, which is the condition for the second definition.[2]

In general, the iterative impedance of port 1 is not equal to the iterative impedance of port 2. They will be equal if the network is symmetrical, however physically symmetry is not a necessary condition for the impedances to be equal.[3]

Examples

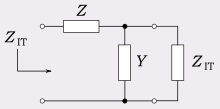
Iterative impedance of a simple generic L-circuit

A simple generic L-circuit is shown in the diagram consisting of a series impedance Z and a shunt admittance Y. The iterative impedance of this network, ZIT, in terms of its output load (also ZIT) is given by,[4]

Z_ \mathrm {IT} = Z + Y \parallel Z_ \mathrm {IT}

and solving for ZIT,

Z_ \mathrm {IT} = {Z \over 2} \pm \sqrt { {Z^2 \over 4} + {Z \over Y} }

Another example is an L-circuit with the components reversed, that is, with the shunt admittance coming first. The analysis of this circuit can be found immediately through duality considerations of the previous example. The iterative admittance, YIT, of this circuit is given by,

Y_ \mathrm {IT} = {Y \over 2} \pm \sqrt { {Y^2 \over 4} + {Y \over Z} }

where,

Y_ \mathrm {IT} = {1 \over Z_ \mathrm {IT} }

The square root term in these expressions cause them to have two solutions. However, only solutions with a positive real part are physically meaningful since passive circuits cannot exhibit negative resistance. This will normally be the positive root.[5]

Relationship to image impedance

Iterative impedance of an infinite ladder of L-circuit sections
Image impedance of an infinite ladder of L-circuit half-sections

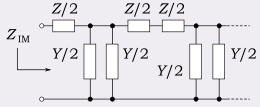
Iterative impedance is a similar concept to image impedance. Whereas an iterative impedance is formed by connecting port 2 of the first two-port network to port 1 of the next, an image impedance is formed by connecting port 2 of the first network to port 2 of the next. Port 1 of the second network is connected to port 1 of the third and so on, each subsequent network being reversed so that like ports always face each other.

It is thus no surprise that there is a relationship between iterative impedances and image impedances. In the L-circuit example for iterative impedance, the square-rooted term is equal to the image impedance of a half section. That is, an L-circuit where the component values are halved. Designating this half-section image impedance as ZIM we have for the L-circuit,[6]

Z_\mathrm {IT} = {Z \over 2} + Z_\mathrm {IM}

The diagrams show this result: an infinite chain of L-sections is identical to an infinite chain of alternately reversed half-sections except for the value of the initial series impedance.

For a symmetrical network, the iterative impedance and image impedance are identical and are the same at both ports. This impedance is sometimes called the network's characteristic impedance, a term usually reserved for transmission lines.[7] The model for a transmission line is an infinite chain of L-sections with infinitesimally small components. A transmission line characteristic impedance is thus the limiting case of a ladder network iterative impedance.[8]

References

  1. ↑ Iyer, p. 340
  2. ↑ Bakshi & Bakshi, pp. 9.4-9.5
  3. ↑ Bird, p. 594
  4. ↑ Walton, p. 209
  5. ↑ Walton, pp. 209-210
  6. ↑ Bakshi & Bakshi, pp. 9.55–9.56
  7. ↑ Bird, pp. 594-595
    • Iyer, p. 345
  8. ↑ Montgomery et al., pp. 112-113

Bibliography

This article is issued from Wikipedia - version of the 5/18/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.