Yff center of congruence
In geometry, the Yff center of congruence is a special point associated with a triangle. This special point is a triangle center and it is designated as the center X(174) in Clark Kimberling's Encyclopedia of Triangle Centers. Peter Yff initiated the study of this triangle center in 1987.[1]
Isoscelizer
An isoscelizer of an angle A in a triangle ABC is a line through points P1 and Q1, where P1 lies on AB and Q1 on AC, such that the triangle AP1Q1 is an isosceles triangle. An isoscelizer of angle A is a line perpendicular to the bisector of angle A. Isoscelizers were invented by Peter Yff in 1963.[2]
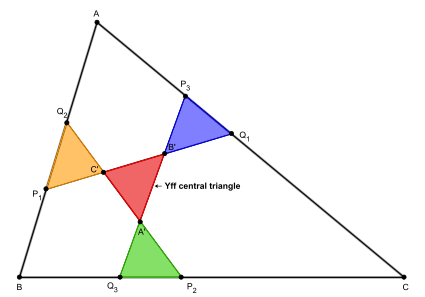
Yff central triangle
Let ABC be any triangle. Let P1Q1 be the isoscelizer of angle A, P2Q2 be the isoscelizer of angle B, and P3Q3 be the isoscelizer of angle C. Let A'B'C' be the triangle formed by the three isoscelizers. The four triangles A'P2Q3, Q1B'P3, P1Q2C', and A'B'C' are always similar.
There is a unique set of three isoscelizers P1Q1, P2Q2, P3Q3 such that the four triangles A'P2Q3, Q1B'P3, P1Q2C', and A'B'C' are congruent. In this special case the triangle A'B'C' formed by the three isoscelizers is called the Yff central triangle of triangle ABC.[3]
The circumcircle of the Yff central triangle is called the Yff central circle of the triangle.
Yff center of congruence
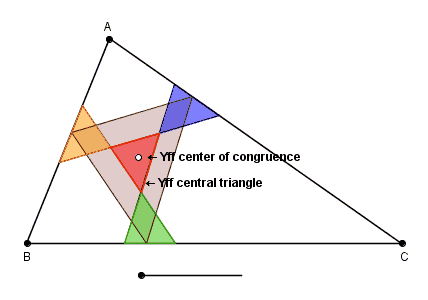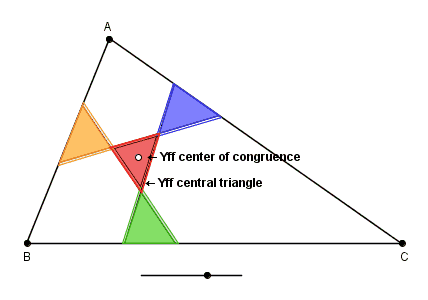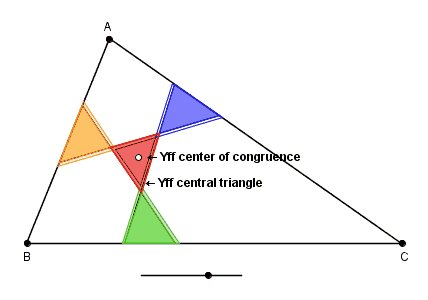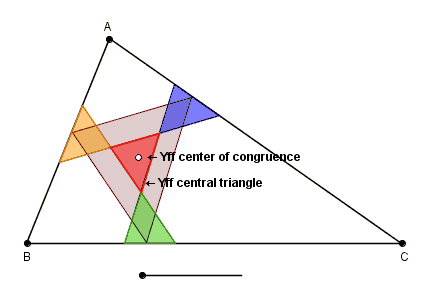
Let ABC be any triangle. Let P1Q1, P2Q2, P3Q3 be the isoscelizers of the angles A, B, C such that the triangle A'B'C' formed by them is the Yff central triangle of triangle ABC. The three isoscelizers P1Q1, P2Q2, P3Q3 are continuously parallel-shifted such that the three triangles A'P2Q3, Q1B'P3, P1Q2C' are always congruent to each other until the triangle A'B'C' formed by the intersections of the isoscelizers reduces to a point. The point to which the triangle A'B'C' reduces to is called the Yff center of congruence of triangle ABC.
Properties
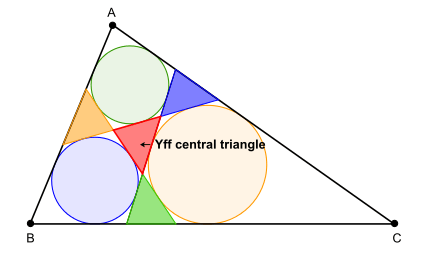
- The trilinear coordinates of the Yff center of congruence are ( sec( A/2 ) : sec ( B/2 ), sec ( C/2 ).[1]
- Any triangle ABC is the triangle formed by the lines which are externally tangent to the three excircles of the Yff central triangle of triangle ABC.
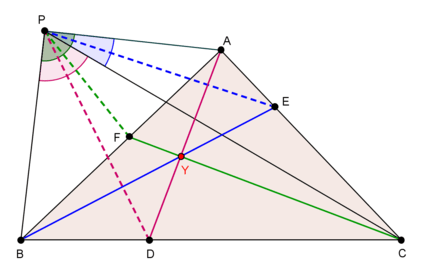
- Let I be the incenter of triangle ABC. Let D be the point on side BC such that ∠BID = ∠DIC, E a point on side CA such that ∠CIE = ∠EIA, and F a point on side AB such that ∠AIF = ∠FIB. Then the lines AD. BE, and CF are concurrent at the Yff center of congruence. This fact gives a geometrical construction for locating the Yff center of congruence.[4]
- A computer assisted search of the properties of the Yff central triangle has generated several interesting results relating to properties of the Yff central triangle.[5]
Generalization
The geometrical construction for locating the Yff center of congruence has an interesting generalization. The generalisation begins with an arbitrary point P in the plane of a triangle ABC. Then points D, E, F are taken on the sides BC, CA, AB such that ∠BPD = ∠DPC, ∠CPE = ∠EPA, and ∠APF = ∠FPB. The generalization asserts that the lines AD, BE, CF are concurrent.[4]
See also
References
- 1 2 Kimberling, Clark. "Yff Center of Congruence". Retrieved 30 May 2012.
- ↑ Weisstein, Eric W. "Isoscelizer". MathWorld--A Wolfram Web Resource. Retrieved 30 May 2012.
- ↑ Weisstein, Eric W. "Yff central triangle". MathWorld--A Wolfram Web Resource. Retrieved 30 May 2012.
- 1 2 Kimberling, Clark. "X(174) = Yff Center of Congruence". Retrieved 2 June 2012.
- ↑ Dekov, Deko (2007). "Yff Center of Congruence". Journal of Computer-Generated Euclidean Geometry. 37: 1–5. Retrieved 30 May 2012.