Island of stability

Measured (boxed) and predicted (shaded) half-lives of isotopes, sorted by number of protons and neutrons. The expected location of the island of stability is circled.

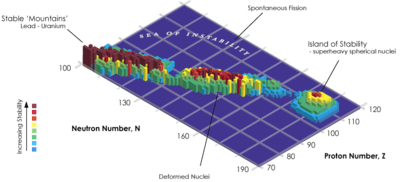
In nuclear physics, the island of stability is the prediction that a set of heavy isotopes with a near magic number of protons and neutrons will temporarily reverse the trend of decreasing stability in elements heavier than uranium. Although predictions of the exact location differ somewhat, Klaus Blaum expects the island of stability to occur in the region near the isotope 300Ubn.[1] Estimates about the amount of stability on the island are usually around a half-life of minutes or days, with some optimistic predictions expecting half-lives of millions of years.[2]

Although the theory has existed since the 1960s, the existence of such superheavy, relatively stable isotopes has not been demonstrated. Like the rest of the superheavy elements, the isotopes on the island of stability have never been found in nature, and so must be created artificially in a nuclear reaction to be studied. However, scientists have not found a way to carry out such a reaction.

With an isotope graph of protons and neutrons with the third dimension of height being the binding energy, the stability region can actually be visualized as a valley (instead of an island).[3]

Theory and origin

One fact should be emphasized from the outset: while the various theoretical predictions about the superheavy nuclei differ as to the expected half-lives and regions of stability, all theoretical predictions are in agreement: superheavy nuclei can exist. Thus, the search for superheavy nuclei remains as a unique, rigorous test of the predictive power of modern theories of the structure of nuclei.

— Seaborg and Loveland, 1987.[4]

The possibility of an "island of stability" was first proposed by Glenn T. Seaborg in the late 1960s.[5] The hypothesis is based upon the nuclear shell model, which implies that the atomic nucleus is built up in "shells" in a manner similar to the structure of the much larger electron shells in atoms. In both cases, shells are just groups of quantum energy levels that are relatively close to each other. Energy levels from quantum states in two different shells will be separated by a relatively large energy gap, so when the number of neutrons and protons completely fills the energy levels of a given shell in the nucleus, the binding energy per nucleon will reach a local maximum and thus that particular configuration will have a longer lifetime than nearby isotopes that do not possess filled shells.[6]

A filled shell would have "magic numbers" of neutrons and protons. One possible magic number of neutrons for spherical nuclei is 184, and some possible matching proton numbers are 114, 120 and 126 – which would mean that the most stable spherical isotopes would be flerovium-298, unbinilium-304 and unbihexium-310. Of particular note is 298Fl, which would be "doubly magic" (both its proton number of 114 and neutron number of 184 are thought to be magic) and thus the most likely to have a very long half-life. (The next lighter doubly magic spherical nucleus is lead-208, the heaviest known stable nucleus and most stable heavy metal.)

Recent research indicates that large nuclei are deformed, causing magic numbers to shift. Hassium-270 is now believed to be a doubly magic deformed nucleus, with deformed magic numbers 108 and 162.[7][8] It has a half-life of 3.6 seconds.

Isotopes have been produced with enough protons to plant them upon an island of stability but with too few neutrons to even place them upon the island's outer "shores". It is possible that these elements possess unusual chemical properties and, if they have isotopes with adequate lifespans, would be available for various practical applications (such as particle accelerator targets and as neutron sources as well). In particular, the very small critical masses of transplutonic elements (possibly as small as grams) implies that if stable elements could be found, they would enable small and compact nuclear bombs either directly or by serving as primaries to help ignite fission/fusion secondaries; this possibility motivated much of the early research and multiple nuclear tests by the United States (including Operation Plowshare) and the Soviet Union aimed at producing such elements.[9]

Half-lives of the highest-numbered elements

All elements with an atomic number above 82 (lead) are unstable, and the "stability" (half-life of the longest-lived known isotope) of elements generally decreases with rising atomic numbers from the relatively stable uranium (92) upwards to the heaviest known element, oganesson (118). The longest-lived observed isotopes of each of the heaviest elements are shown in the following table.

Known isotopes of elements 83 through 118[10][11][12]
Number Name Longest-lived
isotope 		Half-life Article
83 Bismuth 209Bi 2 × 1019 years Isotopes of bismuth
84 Polonium 209Po 130 years Isotopes of polonium
85 Astatine 210At 8 hours Isotopes of astatine
86 Radon 222Rn 3.824 days Isotopes of radon
87 Francium 223Fr 22.0 min Isotopes of francium
88 Radium 226Ra 1600 years Isotopes of radium
89 Actinium 227Ac 21.77 years Isotopes of actinium
90 Thorium 232Th 1.41 × 1010 years Isotopes of thorium
91 Protactinium 231Pa 32800 years Isotopes of protactinium
92 Uranium 238U 4.47 × 109 years Isotopes of uranium
93 Neptunium 237Np 2.14 × 106 years Isotopes of neptunium
94 Plutonium 244Pu 8.0 × 107 years Isotopes of plutonium
95 Americium 243Am 7400 years Isotopes of americium
96 Curium 247Cm 1.6 × 107 years Isotopes of curium
97 Berkelium 247Bk 1000 years Isotopes of berkelium
98 Californium 251Cf 900 years Isotopes of californium
99 Einsteinium 252Es 470 days Isotopes of einsteinium
100 Fermium 257Fm 100.5 days Isotopes of fermium
101 Mendelevium 258Md 51.5 days Isotopes of mendelevium
102 Nobelium 259No 58 minutes Isotopes of nobelium
103 Lawrencium 266Lr 11 hours Isotopes of lawrencium
104 Rutherfordium 267Rf 1.3 hours Isotopes of rutherfordium
105 Dubnium 268Db 1.3 days Isotopes of dubnium
106 Seaborgium 269Sg 3.1 minutes Isotopes of seaborgium
107 Bohrium 270Bh 61 seconds Isotopes of bohrium
108 Hassium 269Hs 9.6 seconds Isotopes of hassium
109 Meitnerium 278Mt 7.6 seconds Isotopes of meitnerium
110 Darmstadtium 281Ds 9.6 seconds Isotopes of darmstadtium
111 Roentgenium 282Rg 2.1 minutes Isotopes of roentgenium
112 Copernicium 285Cn 29 seconds Isotopes of copernicium
113 Nihonium 286Nh 19.6 seconds Isotopes of nihonium
114 Flerovium 289Fl 2.6 seconds Isotopes of flerovium
115 Moscovium 289Mc 220 milliseconds Isotopes of moscovium
116 Livermorium 293Lv 61 milliseconds Isotopes of livermorium
117 Tennessine 294Ts 78 milliseconds Isotopes of tennessine
118 Oganesson 294Og 890 microseconds Isotopes of oganesson

(Note that for elements 108–118, the longest-lived known isotope is always the heaviest or second-heaviest (115) discovered thus far. This makes it seem likely that there are longer-lived undiscovered isotopes among the even heavier ones.)

For comparison, the shortest-lived element with atomic number below 100 is francium (element 87) with a half-life of 22 minutes.

The half-lives of nuclei in the island of stability itself are unknown since none of the isotopes that would be "on the island" have been observed. Many physicists think they are relatively short, on the order of minutes or days.[2] Some theoretical calculations indicate that their half-lives may be long, on the order of 109 years.[13]

The alpha-decay half-lives of 1700 nuclei with 100 ≤ Z ≤ 130 have been calculated in a quantum tunneling model with both experimental and theoretical alpha-decay Q-values.[14][15][16][17][18][19] The theoretical calculations are in good agreement with the available experimental data.

A possible stronger decay mode for the heaviest superheavies was shown to be cluster decay by Dorin N. Poenaru, R.A. Gherghescu, and Walter Greiner.[20]

Periodic table with elements colored according to the half-life of their most stable isotope.
  Stable elements.
  Radioactive elements with half-lives of over four million years.
  Half-lives between 800 and 34,000 years.
  Half-lives between 1 day and 103 years.
  Half-lives ranging between several minutes and 1 day.
  Half-lives less than several minutes.

Islands of relative stability

Actinides and fission products by half-life
Actinides[21] by decay chain Half-life
range (y)		 Fission products of 235U by yield[22]
4n 4n+1 4n+2 4n+3
4.5–7% 0.04–1.25% <0.001%
228Ra№ 4–6 † 155Euþ
244Cmƒ 241Puƒ 250Cf 227Ac№ 10–29 90Sr 85Kr 113mCdþ
232Uƒ 238Puƒ№ 243Cmƒ 29–97 137Cs 151Smþ 121mSn
248Bk[23] 249Cfƒ 242mAmƒ 141–351

No fission products
have a half-life
in the range of
100–210 k years ...

241Amƒ 251Cfƒ[24] 430–900
226Ra№ 247Bk 1.3 k – 1.6 k
240Puƒ№ 229Th№ 246Cmƒ 243Amƒ 4.7 k – 7.4 k
245Cmƒ 250Cm 8.3 k – 8.5 k
239Puƒ№ 24.1 k
230Th№ 231Pa№ 32 k – 76 k
236Npƒ 233Uƒ№ 234U№ 150 k – 250 k ‡ 99Tc₡ 126Sn
248Cm 242Puƒ 327 k – 375 k 79Se₡
1.53 M 93Zr
237Npƒ№ 2.1 M – 6.5 M 135Cs₡ 107Pd
236U№ 247Cmƒ 15 M – 24 M 129I₡
244Pu№ 80 M

... nor beyond 15.7 M years[25]

232Th№ 238U№ 235Uƒ№ 0.7 G – 14.1 G

Legend for superscript symbols
₡  has thermal neutron capture cross section in the range of 8–50 barns
ƒ  fissile
m  metastable isomer
№  naturally occurring radioactive material (NORM)
þ  neutron poison (thermal neutron capture cross section greater than 3k barns)
†  range 4–97 y: Medium-lived fission product
‡  over 200,000 y: Long-lived fission product

Region of relative stability: radium-226 to einsteinium-252
       88 89 90 91 92 93 94 95 96 97 98 99       
   
 154 
Half-life Key
  1   10  100 
  1k  10k 100k
  1M  10M 100M
  1G  10G (a)
 250Cm 252Cf  154 
 153  251Cf 252Es  153 
 152  248Cm 250Cf  152 
 151  247Cm 248Bk 249Cf  151 
 150  244Pu 246Cm 247Bk  150 
 149  245Cm  149 
 148  242Pu 243Am 244Cm  148 
 147  241Pu
242m⁂
243Cm  147 
 146  238U  240Pu 241Am  146 
 145  239Pu  145 
 144  236U  237Np 238Pu  144 
 143  235U  236Np  143 
 142  232Th 234U  235Np 236Pu  142 
 141  233U   141 
 140  228Ra 230Th 231Pa 232U 
Table Axes
Neutrons (N)
Protons (Z)
  140 
 139  229Th  139 
 138  226Ra 227Ac 228Th  138 
   
       88 89 90 91 92 93 94 95 96 97 98 99       
Only isotopes with a half-life of at least one year are listed.

232
Th (thorium), 235
U and 238
U (uranium) are the only naturally occurring isotopes beyond bismuth that are relatively stable over the current lifespan of the universe. Even bismuth was found to be slightly unstable in 2003, with an α-emission half-life of 1.9×1019 years for 209
Bi. All elements beyond bismuth have relatively or very unstable isotopes: astatine, radon, and francium are extremely short-lived (and only have half-lives longer than isotopes of the heaviest elements found so far). Even thorium, with the largest known half-life in this region (1.4×1010 years for 232
Th), is still about a billion times shorter than 209
Bi, so the main periodic table ends there.

By geographical analogy, bismuth is the shore edge of a continent. A continental shelf continues though, with shallows beginning at radium (see 'map' at right) that rapidly drop off again after californium. Significant islands appear at thorium and uranium, and with minor ones (i.e. neptunium, plutonium and curium) form an archipelago. All of this is surrounded by a "sea of instability".[26] As can be seen from the table, there is a significantly large gap between the half-lives of the longest-lived actinide isotopes (the primordial 232Th, 238U, 235U, and 244Pu, and the long-lived 236U, 247Cm, and 237Np) and those of the others.

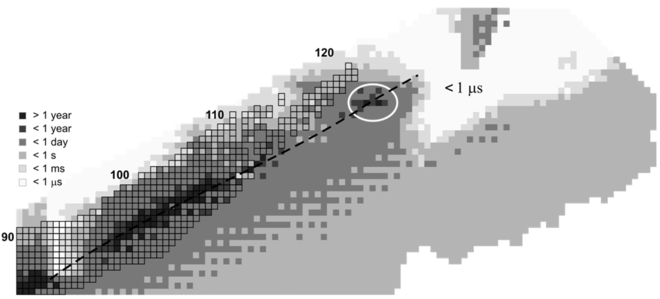
A 3D graph of stability of elements vs. number of protons Z and neutrons N, showing a "mountain chain" running diagonally through the graph from the low to high numbers, as well as an "island of stability" at high N and Z.
3-dimensional rendering of the theoretical island of stability around N=178 and Z=112

Current theoretical investigation indicates that in the region Z = 106–108 and N ≈ 160–164, a small ‘island/peninsula’ might be stable with respect to fission and beta decay, such superheavy nuclei undergoing only alpha decay.[15][16][17] Also, 298
Fl is not the center of the magic island as predicted earlier.[27] On the contrary, the nucleus with Z = 110, N = 183 (293Ds) appears to be near the center of a possible 'magic island' (Z = 104–116, N ≈ 176–186). In the N ≈ 162 region the beta-stable, fission survived 268
Sg is predicted to have alpha-decay half-life ~3.2 hours that is greater than that (~28 s) of the deformed doubly magic 270
Hs.[28] The superheavy nucleus 268
Sg has not been produced in the laboratory as yet (2009). For superheavy nuclei with Z > 116 and N ≈ 184 the alpha-decay half-lives are predicted to be less than one second. The nuclei with Z = 120, 124, 126 and N = 184 (304Ubn, 308Ubq, and 310Ubh) are predicted to form spherical doubly magic nuclei and be stable with respect to fission.[29] Calculations in a quantum tunneling model show that such superheavy nuclei would undergo alpha decay within microseconds or less.[15][16][17]

Synthesis problems

The manufacture of nuclei on the island of stability proves to be very difficult because the nuclei available as starting materials do not deliver the necessary sum of neutrons. For the synthesis of isotope 298 of flerovium, one could use an isotope of plutonium and one of calcium that together have a sum of at least 298 nucleons; for example, calcium-50 and plutonium-248. These and heavier isotopes are not available in measurable quantities, making production virtually impossible with current methods. The same problem exists for the other possible combinations of isotopes needed to generate elements on the island using target-projectile methods. It may be possible to generate the isotope 298 of flerovium, if the multi-nucleon transfer reactions would work in low-energy collisions of actinide nuclei.[30] One of these reactions may be:

248
Cm
 + 238
U
 → 298
Fl
 + 186
W
 + 2 1
0n

Hypothetical second island

At the 235th national meeting of the American Chemical Society in 2008, the idea of a second island of stability was presented by Yuri Oganessian. This new island would be centered on element 164 (unhexquadium), especially the isotope 482Uhq, with a stability similar to that of flerovium.[31] It is thought that to be able to synthesize these elements, a new, stronger particle accelerator would be needed.[32]

See also

References

  1. ↑ "Superheavy, and yet stable". Max-Planck-Gesellschaft. 23 August 2012. Retrieved 23 June 2013. We expect [the island of stability] at around element 120," says Blaum, "and to be more precise, in a nucleus with around 180 neutrons.
  2. 1 2 "Superheavy Element 114 Confirmed: A Stepping Stone to the Island of Stability". Berkeley Lab. 24 September 2009. Retrieved 25 October 2016.
  3. ↑ CEA Sciences. The Valley of Stability (video) - a virtual "flight" through 3D representation of the nuclide chart. YouTube. Event occurs at 3:12.
  4. ↑ Seaborg, G. T. (1987). "Superheavy elements". Contemporary Physics. 28: 33–48. Bibcode:1987ConPh..28...33S. doi:10.1080/00107518708211038.
  5. ↑ "The Island of Stability?". Retrieved 2012-07-24.
  6. ↑ Nave, R. "Shell Model of Nucleus". HyperPhysics. Department of Physics and Astronomy, Georgia State University. Retrieved 22 January 2007.
  7. ↑ Dvořák, J. (2007). Decay properties of nuclei close to Z = 108 and N = 162 (PhD thesis). Technische Universität München.
  8. ↑ Dvorak, J.; et al. (2006). "Doubly Magic Nucleus 270
    108    Hs
    162    ". Physical Review Letters. 97 (24): 242501. Bibcode:2006PhRvL..97x2501D. doi:10.1103/PhysRevLett.97.242501. PMID 17280272.
  9. ↑ Gsponer, A.; Hurni, J.-P. (2009). Fourth Generation Nuclear Weapons: The physical principles of thermonuclear explosives, inertial confinement fusion, and the quest for fourth generation nuclear weapons (3rd printing of the 7th ed.). pp. 129–133.
  10. ↑ Emsley, J. (2001). Nature's Building Blocks. Oxford University Press. pp. 143−144, 458. ISBN 0-19-850340-7.
  11. ↑ Khuyagbaatar, J. (2014). "48Ca+249Bk Fusion Reaction Leading to Element Z = 117: Long-Lived α-Decaying 270Db and Discovery of 266Lr". Physical Review Letters. 112: 172501. Bibcode:2014PhRvL.112q2501K. doi:10.1103/PhysRevLett.112.172501.
  12. ↑ Witze, A. (6 April 2010). "Superheavy element 117 makes debut". ScienceNews. Retrieved 2010-04-06.
  13. ↑ Oganessian, Y. (2012). "Nuclei in the "Island of Stability" of Superheavy Elements". Journal of Physics: Conference Series. 337 (1): 012005. Bibcode:2012JPhCS.337a2005O. doi:10.1088/1742-6596/337/1/012005.
  14. ↑ Chowdhury, P. R.; Samanta, C.; Basu, D. N. (2006). "α decay half-lives of new superheavy elements". Physical Review C. 73: 014612. arXiv:nucl-th/0507054Freely accessible. Bibcode:2006PhRvC..73a4612C. doi:10.1103/PhysRevC.73.014612.
  15. 1 2 3 Samanta, C.; Chowdhury, P. R.; Basu, D. N. (2007). "Predictions of alpha decay half lives of heavy and superheavy elements". Nuclear Physics A. 789: 142–154. arXiv:nucl-th/0703086Freely accessible. Bibcode:2007NuPhA.789..142S. doi:10.1016/j.nuclphysa.2007.04.001.
  16. 1 2 3 Chowdhury, P. R.; Samanta, C.; Basu, D. N. (2008). "Search for long lived heaviest nuclei beyond the valley of stability". Physical Review C. 77 (4): 044603. arXiv:0802.3837Freely accessible. Bibcode:2008PhRvC..77d4603C. doi:10.1103/PhysRevC.77.044603.
  17. 1 2 3 Chowdhury, P. R.; Samanta, C.; Basu, D. N. (2008). "Nuclear half-lives for α-radioactivity of elements with 100 ≤ Z ≤ 130". Atomic Data and Nuclear Data Tables. 94 (6): 781–806. arXiv:0802.4161Freely accessible. Bibcode:2008ADNDT..94..781C. doi:10.1016/j.adt.2008.01.003.
  18. ↑ Chowdhury, P. R.; Basu, D. N.; Samanta, C. (2007). "α decay chains from element 113". Physical Review C. 75 (4): 047306. arXiv:0704.3927Freely accessible. Bibcode:2007PhRvC..75d7306C. doi:10.1103/PhysRevC.75.047306.
  19. ↑ Samanta, C.; Basu, D. N.; Chowdhury, P. R. (2007). "Quantum tunneling in 277112 and its alpha-decay chain". Journal of the Physical Society of Japan. 76 (12): 124201. arXiv:0708.4355Freely accessible. Bibcode:2007JPSJ...76l4201S. doi:10.1143/JPSJ.76.124201.
  20. ↑ Poenaru, D. N.; Gherghescu, R. A.; Greiner, W. (2011). "Heavy-Particle Radioactivity of Superheavy Nuclei". Physical Review Letters. 107 (6): 062503. arXiv:1106.3271Freely accessible. Bibcode:2011PhRvL.107f2503P. doi:10.1103/PhysRevLett.107.062503. PMID 21902317.
  21. ↑ Plus radium (element 88). While actually a sub-actinide, it immediately precedes actinium (89) and follows a three-element gap of instability after polonium (84) where no isotopes have half-lives of at least four years (the longest-lived isotope in the gap is radon-222 with a half life of less than four days). Radium's longest lived isotope, at 1,600 years, thus merits the element's inclusion here.
  22. ↑ Specifically from thermal neutron fission of U-235, e.g. in a typical nuclear reactor.
  23. ↑ Milsted, J.; Friedman, A. M.; Stevens, C. M. (1965). "The alpha half-life of berkelium-247; a new long-lived isomer of berkelium-248". Nuclear Physics. 71 (2): 299. doi:10.1016/0029-5582(65)90719-4.
    "The isotopic analyses disclosed a species of mass 248 in constant abundance in three samples analysed over a period of about 10 months. This was ascribed to an isomer of Bk248 with a half-life greater than 9 y. No growth of Cf248 was detected, and a lower limit for the β− half-life can be set at about 104 y. No alpha activity attributable to the new isomer has been detected; the alpha half-life is probably greater than 300 y."
  24. ↑ This is the heaviest isotope with a half-life of at least four years before the "Sea of Instability".
  25. ↑ Excluding those "classically stable" isotopes with half-lives significantly in excess of 232Th; e.g., while 113mCd has a half-life of only fourteen years, that of 113Cd is nearly eight quadrillion years.
  26. ↑ Note graphic: Known and predicted regions of nuclear stability, surrounded by a "sea" of instability. cf. the Chart of Nuclides by half-life.
  27. ↑ Nilsson, S. G.; et al. (1969). "On the nuclear structure and stability of heavy and superheavy elements". Nuclear Physics A. 131 (1): 1–66. Bibcode:1969NuPhA.131....1N. doi:10.1016/0375-9474(69)90809-4.
  28. ↑ Dvorak, J.; et al. (2006). "Doubly Magic Nucleus 270
    108    Hs
    162    ". Physical Review Letters. 97 (24). Bibcode:2006PhRvL..97x2501D. doi:10.1103/PhysRevLett.97.242501. PMID 17280272.
  29. ↑ Ćwiok, S.; Heenen, P.-H.; Nazarewicz, W. (2005). "Shape coexistence and triaxiality in the superheavy nuclei" (PDF). Nature. 433 (7027): 705–709. Bibcode:2005Natur.433..705C. doi:10.1038/nature03336. PMID 15716943.
  30. ↑ Zagrebaev, V.; Greiner, W. (2008). "Synthesis of superheavy nuclei: A search for new production reactions". Physical Review C. 78 (3). arXiv:0807.2537Freely accessible. Bibcode:2008PhRvC..78c4610Z. doi:10.1103/PhysRevC.78.034610.
  31. ↑ Grumann, J.; Mosel, U.; Fink, B.; Greiner, W. (1969). "Investigation of the stability of superheavy nuclei around Z = 114 and Z = 164". Zeitschrift für Physik. 228: 371–386. Bibcode:1969ZPhy..228..371G. doi:10.1007/BF01406719.
  32. ↑ "Nuclear scientists eye future landfall on a second 'island of stability'". Eurekalert.org. 2008-04-06. Retrieved 2014-05-02.

External links

This article is issued from Wikipedia - version of the 12/4/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.