Hyperstability

In stability theory, hyperstability is a property of a system that requires the state vector to remain bounded if the inputs are restricted to belonging to a subset of the set of all possible inputs.[1]

Definition:[2] A system is hyperstable if there are two constants 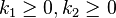k_1 \ge 0, k_2 \ge 0 such that any state trajectory of the system satisfies the inequality:

\| x(t) \| < k_1 \|x(0)\| + k_2, \, \forall t \ge 0

References

  1. ↑ Brian D. O Anderson, "A Simplified Viewpoint of Hyperstability", IEEE Transactions on Automatic Control, June 1968
  2. ↑ Zinober, Deterministic control of uncertain systems, 1990

See also


This article is issued from Wikipedia - version of the 3/1/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.