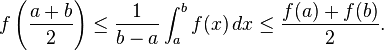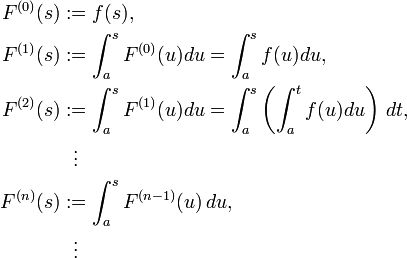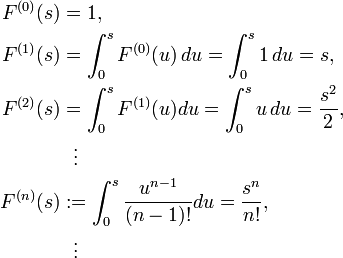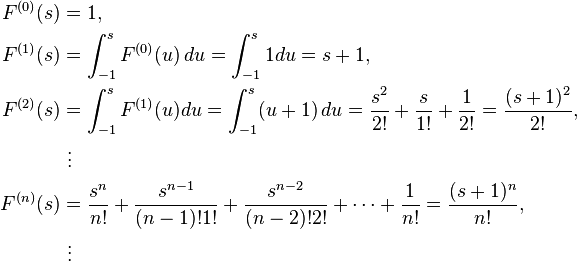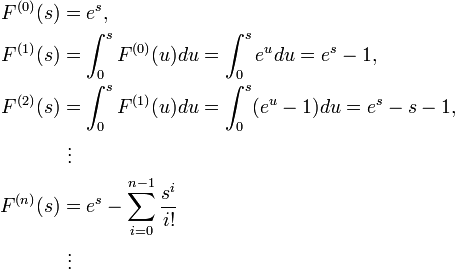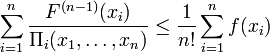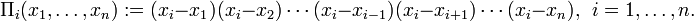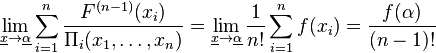Hermite–Hadamard inequality

Not to be confused with Hadamard's inequality.

In mathematics, the Hermite–Hadamard inequality, named after Charles Hermite and Jacques Hadamard and sometimes also called Hadamard's inequality, states that if a function ƒ : [a, b] → R is convex, then the following chain of inequalities hold:

f\left( \frac{a+b}{2}\right) \le \frac{1}{b - a}\int_a^b f(x)\,dx \le \frac{f(a) + f(b)}{2}.

Generalisations - The concept of a sequence of iterated integrals

Suppose that −∞ < a < b < ∞, and let f:[a, b] → ℝ be an integrable real function. Under the above conditions the following sequence of functions is called the sequence of iterated integrals of f,where a ≤ s ≤ b.:

\begin{align} F^{(0)}(s) & := f(s), \\ F^{(1)}(s) & := \int^s_a F^{(0)}(u)du=\int^s_a f(u)du, \\ F^{(2)}(s) & := \int^s_a F^{(1)}(u)du=\int^s_a \left( \int^t_a f(u)du \right ) \, dt, \\ & \ \ \vdots \\ F^{(n)}(s) & := \int^s_a F^{(n-1)}(u) \, du, \\ & {}\ \ \vdots \end{align}

Example 1

Let [a, b] = [0, 1] and f(s) ≡ 1. Then the sequence of iterated integrals of 1 is defined on [0, 1], and

\begin{align} F^{(0)}(s) & = 1, \\ F^{(1)}(s) & = \int^s_0 F^{(0)}(u) \, du=\int^s_0 1 \, du=s, \\ F^{(2)}(s) & = \int^s_0 F^{(1)}(u)du=\int^s_0 u \, du={s^2 \over 2}, \\ & {} \ \ \vdots \\ F^{(n)}(s) & := \int^s_0 {u^{n-1}\over (n-1)!}du={s^n \over n!}, \\ & {} \ \ \vdots \end{align}

Example 2

Let [a,b] = [−1,1] and f(s) ≡ 1. Then the sequence of iterated integrals of 1 is defined on [−1, 1], and

\begin{align} F^{(0)}(s) & = 1, \\ F^{(1)}(s) & = \int^s_{-1} F^{(0)}(u) \, du=\int^s_{-1} 1 du=s+1, \\ F^{(2)}(s) & = \int^s_{-1} F^{(1)}(u)du=\int^s_{-1} (u+1) \, du={s^2 \over 2!}+{s \over 1!}+{1 \over 2!}={(s+1)^2 \over 2!}, \\ & {} \ \vdots \\ F^{(n)}(s) & = {s^n \over n!}+{s^{n-1}\over {(n-1)!1!}}+{s^{n-2} \over (n-2)!2!}+ \dots +{1 \over n!} ={(s+1)^n \over n!}, \\ & {} \ \vdots \end{align}

Example 3

Let [a, b] = [0, 1] and f(s) = es. Then the sequence of iterated integrals of f is defined on [0, 1], and

\begin{align} F^{(0)}(s) & = e^s, \\ F^{(1)}(s) & = \int^s_0 F^{(0)}(u)du=\int^s_0 e^u du=e^s-1, \\ F^{(2)}(s) & = \int^s_0 F^{(1)}(u)du=\int^s_0 (e^u-1) du=e^s-s-1, \\ & {} \ \vdots \\ F^{(n)}(s) & = e^s-\sum_{i=0}^{n-1}\frac {s^i}{i!} \\ & {}\ \vdots \end{align}

Theorem

Suppose that −∞ < a < b < ∞, and let f:[a,b]→R be a convex function, a < xi < b, i = 1, ..., n, such that xi ≠ xj, if i ≠ j. Then the following holds:

\sum_{i=1}^n \frac {F^{(n-1)}(x_i)}{\Pi_i(x_1,\dots,x_n)}\leq \frac {1}{n!} \sum_{i=1}^n f(x_i)

where

\Pi_i(x_1,\dots,x_n):=(x_i-x_1)(x_i-x_2)\cdots(x_i-x_{i-1})(x_i-x_{i+1})\cdots(x_i-x_n),\ \ i=1,\dots,n.

In the concave case ≤ is changed to ≥.

Remark 1. If f is convex in the strict sense then ≤ is changed to < and equality holds iff f is linear function.

Remark 2. The inequality is sharp in the following limit sense: let 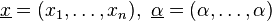\underline x =(x_1,\ldots,x_n),\ \underline \alpha = (\alpha, \ldots ,\alpha) and \ a<\alpha<b.
Then the limit of the left side exists and

\lim_{\underline x \to \underline \alpha} \sum_{i=1}^n \frac{F^{(n-1)}(x_i)}{\Pi_i(x_1,\ldots,x_n)}=\lim_{\underline x \to \underline \alpha}\frac{1}{n!}\sum_{i=1}^n f(x_i)= \frac{f(\alpha)}{(n-1)!}

References

This article is issued from Wikipedia - version of the 3/5/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.