Hénon-Heiles System
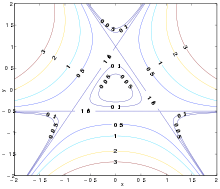
While at Princeton in 1962, Michel Hénon and Carl Heiles worked on the non-linear motion of a star around a galactic center where the motion is restricted to a plane. In 1964 they published an article [1] titled 'The applicability of the third integral of motion: Some numerical experiments'. Their original idea was to find a third integral of motion in a galactic dynamics. For that purpose they took a simplified two-dimensional nonlinear axi-symmetric potential and found that the third integral existed only for a limited number of initial conditions. In the modern perspective these initial conditions which do not have the third integral motion are called chaotic orbits.
Introduction
The Hénon-Heiles Potential can be expressed as[2]
The Hénon-Heiles Hamiltonian can be written as
The Hénon-Heiles System (HHS) is defined by the following four equations:
In the classical chaos community, the value of the parameter is usually taken as unity. Since HHS is specified in , we need a Hamiltonian of degrees of freedom two to model it. It can be solved for some cases using Painlevé Analysis.
Quantum Henon-Heiles Hamiltonian
In the quantum case the Henon-Heiles Hamiltonian can be written as a two-dimensional Schrödinger equation.
The corresponding two-dimensional Schrödinger equation is given by
- .
Wada Property of the Exit Basins
Hénon-Heiles system shows rich dynamical behavior. Usually the wada property cannot be seen in the Hamiltonian system but Hénon-Heiles exit basin shows an interesting wada property. It can be seen that when the energy is greater than the critical energy, the Hénon-Heiles system has three exit basins. In 2001 M. A. F. Sanjuán et al.[3] had shown that in the Henon-Heiles system the exit basins have the wada property.
References
- ↑ Hénon, M.; Heiles, C. (1964). "The applicability of the third integral of motion: Some numerical experiments". The Astronomical Journal. 69: 73–79. Bibcode:1964AJ.....69...73H. doi:10.1086/109234.
- ↑ Hénon, Michel (1983), "Numerical exploration of Hamiltonian Systems", in Iooss, G., Chaotic Behaviour of Deterministic Systems, Elsevier Science Ltd, pp. 53–170, ISBN 044486542X
- ↑ Wada basins and chaotic invariant sets in the Henon-Heiles system, Phys. Rev. E 64, 066208 (2001)