Godunov's theorem

In numerical analysis and computational fluid dynamics, Godunov's theorem — also known as Godunov's order barrier theorem — is a mathematical theorem important in the development of the theory of high resolution schemes for the numerical solution of partial differential equations.

The theorem states that:

Linear numerical schemes for solving partial differential equations (PDE's), having the property of not generating new extrema (monotone scheme), can be at most first-order accurate.

Professor Sergei K. Godunov originally proved the theorem as a Ph.D. student at Moscow State University. It is his most influential work in the area of applied and numerical mathematics and has had a major impact on science and engineering, particularly in the development of methods used in computational fluid dynamics (CFD) and other computational fields. One of his major contributions was to prove the theorem (Godunov, 1954; Godunov, 1959), that bears his name.

The theorem

We generally follow Wesseling (2001).

Aside

Assume a continuum problem described by a PDE is to be computed using a numerical scheme based upon a uniform computational grid and a one-step, constant step-size, M grid point, integration algorithm, either implicit or explicit. Then if $x_{j} = j\,\Delta x \$ and $t^{n} = n\,\Delta t \$ , such a scheme can be described by

\sum\limits_{m=1}^{M} {\beta _m } \varphi _{j + m}^{n + 1} = \sum\limits_{m=1}^{M} {\alpha _m \varphi _{j + m}^n }. \quad \quad ( 1)

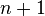In other words, the solution $\varphi _j^{n + 1} \$ at time $n + 1$ and location 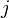$j$ is a linear function of the solution at the previous time step 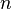$n$ . We assume that $\beta _m \$ determines $\varphi _j^{n + 1} \$ uniquely. Now, since the above equation represents a linear relationship between $\varphi _j^{n } \$ and $\varphi _j^{n + 1} \$ we can perform a linear transformation to obtain the following equivalent form,

\varphi _j^{n + 1} = \sum\limits_m^{M} {\gamma _m \varphi _{j + m}^n }. \quad \quad ( 2)

Theorem 1: Monotonicity preserving

The above scheme of equation (2) is monotonicity preserving if and only if

\gamma _m \ge 0,\quad \forall m . \quad \quad ( 3)

Proof - Godunov (1959)

Case 1: (sufficient condition)

Assume (3) applies and that $\varphi _j^n \$ is monotonically increasing with $j \$ .

Then, because $\varphi _j^n \le \varphi _{j + 1}^n \le \cdots \le \varphi _{j + m}^n$ it therefore follows that $\varphi _j^{n + 1} \le \varphi _{j + 1}^{n + 1} \le \cdots \le \varphi _{j + m}^{n + 1} \$ because

\varphi _j^{n + 1} - \varphi _{j - 1}^{n + 1} = \sum\limits_m^{M} {\gamma _m \left( {\varphi _{j + m}^n - \varphi _{j + m - 1}^n } \right)} \ge 0 . \quad \quad ( 4)

This means that monotonicity is preserved for this case.

Case 2: (necessary condition)

We prove the necessary condition by contradiction. Assume that $\gamma _p^{} < 0 \$ for some $p \$ and choose the following monotonically increasing $\varphi_j^n \quad$ ,

\varphi _i^n = 0, \quad i < k;\quad \varphi _i^n = 1, \quad i \ge k . \quad \quad ( 5)

Then from equation (2) we get

\varphi _j^{n + 1} - \varphi _{j-1}^{n+1} = \sum\limits_m^M {\gamma _m } \left( {\varphi _{j + m}^{n} - \varphi _{j + m - 1}^{n} } \right) = \left\{ {\begin{array}{*{20}c} {0,} & {\left[ {j + m \ne k} \right]} \\ {\gamma _m ,} & {\left[ {j + m = k} \right]} \\ \end{array}} \right . \quad \quad ( 6)

Now choose $j=k-p \$ , to give

\varphi _{k-p}^{n + 1} - \varphi _{k-p-1}^{n + 1} = {\gamma _p \left( {\varphi _{k}^n - \varphi _{k - 1}^n } \right)} < 0 , \quad \quad ( 7)

which implies that $\varphi _j^{n + 1} \$ is NOT increasing, and we have a contradiction. Thus, monotonicity is NOT preserved for $\gamma _p < 0 \$ , which completes the proof.

Theorem 2: Godunov’s Order Barrier Theorem

Linear one-step second-order accurate numerical schemes for the convection equation

{{\partial \varphi } \over {\partial t}} + c{ { \partial \varphi } \over {\partial x}} = 0 , \quad t > 0, \quad x \in \mathbb{R} \quad \quad (10)

cannot be monotonicity preserving unless

\sigma = \left| c \right|{{\Delta t} \over {\Delta x}} \in \mathbb{ N} , \quad \quad (11)

where $\sigma \$ is the signed Courant–Friedrichs–Lewy condition (CFL) number.

Proof - Godunov (1959)

Assume a numerical scheme of the form described by equation (2) and choose

\varphi \left( {0,x} \right) = \left( {{x \over {\Delta x}} - {1 \over 2}} \right)^2 - {1 \over 4}, \quad \varphi _j^0 = \left( {j - {1 \over 2}} \right)^2 - {1 \over 4} . \quad \quad (12)

The exact solution is

\varphi \left( {t,x} \right) = \left( {{{x - ct} \over {\Delta x}} - {1 \over 2}} \right)^2 - {1 \over 4} . \quad \quad (13)

If we assume the scheme to be at least second-order accurate, it should produce the following solution exactly

\varphi _j^1 = \left( {j - \sigma - {1 \over 2}} \right)^2 - {1 \over 4}, \quad \varphi _j^0 = \left( {j - {1 \over 2}} \right)^2 - {1 \over 4}. \quad \quad (14)

Substituting into equation (2) gives:

\left( {j - \sigma - {1 \over 2}} \right)^2 - {1 \over 4} = \sum\limits_m^{M} {\gamma _m \left\{ {\left( {j + m - {1 \over 2}} \right)^2 - {1 \over 4}} \right\}}. \quad \quad (15)

Suppose that the scheme IS monotonicity preserving, then according to the theorem 1 above, $\gamma _m \ge 0 \$ .

Now, it is clear from equation (15) that

\left( {j - \sigma - {1 \over 2}} \right)^2 - {1 \over 4} \ge 0, \quad \forall j . \quad \quad (16)

Assume $\sigma > 0, \quad \sigma \notin \mathbb{ N} \$ and choose $j \$ such that $j > \sigma > \left( j - 1 \right) \$ . This implies that $\left( {j - \sigma } \right) > 0 \$ and $\left( {j - \sigma - 1} \right) < 0 \$ .

It therefore follows that,

\left( {j - \sigma - {1 \over 2}} \right)^2 - {1 \over 4} = \left( j - \sigma \right) \left(j - \sigma - 1 \right) < 0, \quad \quad (17)

which contradicts equation (16) and completes the proof.

The exceptional situation whereby $\sigma = \left| c \right|{{\Delta t} \over {\Delta x}} \in \mathbb{N} \$ is only of theoretical interest, since this cannot be realised with variable coefficients. Also, integer CFL numbers greater than unity would not be feasible for practical problems.

References

Godunov, Sergei K. (1954), Ph.D. Dissertation: Different Methods for Shock Waves, Moscow State University.
Godunov, Sergei K. (1959), A Difference Scheme for Numerical Solution of Discontinuous Solution of Hydrodynamic Equations, Math. Sbornik, 47, 271-306, translated US Joint Publ. Res. Service, JPRS 7226, 1969.
Wesseling, Pieter (2001), Principles of Computational Fluid Dynamics, Springer-Verlag.

Godunov's theorem

The theorem

See also

References

Further reading