Gino Fano
| Gino Fano | |
|---|---|
 | |
| Born |
5 January 1871 Mantua, Italy |
| Died |
8 November 1952 (aged 81) Verona, Italy |
| Nationality | Italian |
| Fields | Mathematics |
| Known for |
Fano postulate Fano plane Fano fibration Fano surface Fano varieties |
Gino Fano (5 January 1871 – 8 November 1952) was an Italian mathematician, best known as the founder of the finite geometry. He was born in Mantua, in Italy and died in Verona, also in Italy.
Fano made various contributions on projective and algebraic geometry. His work in the foundations of geometry predates the similar, but more popular, work of David Hilbert by about a decade.
He was the father of physicist Ugo Fano and mathematician Robert Fano and uncle to physicist and mathematician Giulio Racah.
Mathematical work
Fano was an early writer in the area of finite projective spaces. In his article[1] on proving the independence of his set of axioms for projective n-space,[2] among other things, he considered the consequences of having a fourth harmonic point be equal to its conjugate. This leads to a configuration of seven points and seven lines contained in a finite three-dimensional space with 15 points, 35 lines and 15 planes, in which each line contained only three points.[1]:114
All the planes in this space consist of seven points and seven lines and are now known as Fano planes:
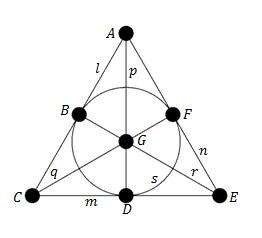
Fano went on to describe finite projective spaces of arbitrary dimension and prime orders.
In 1907 Gino Fano contributed two articles to Part III of Klein's encyclopedia. The first (SS. 221–88) was a comparison of analytic geometry and synthetic geometry through their historic development in the 19th century. The second (SS. 282–388) was on continuous groups in geometry and group theory as a unifying principle in geometry.[3]
Notes
- 1 2 Fano, G. (1892), "Sui postulati fondamentali della geometria proiettiva", Giornale di Matematiche, 30: 106–132
- ↑ Collino, Conte & Verra 2013, p. 6
- ↑ Fano, Gino (1907). "Kontinuierliche geometrische Gruppen. Die Gruppentheorie als geometrisches Einteilungsprinzip". Encyclopädie der mathematischen Wissenschaften. 3.1.1: 289–388. doi:10.1007/978-3-663-16027-4_5.
References
- Collino, Alberto; Conte, Alberto; Verra, Alessandro (2013). "On the life and scientific work of Gino Fano". arXiv:1311.7177
 .
. - Grattan-Guinness, Ivor (2000). The Search for Mathematical Roots 1870–1940. Princeton University Press.
External links
- O'Connor, John J.; Robertson, Edmund F., "Gino Fano", MacTutor History of Mathematics archive, University of St Andrews.
- Gino Fano at the Mathematics Genealogy Project