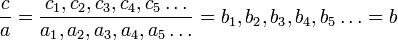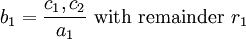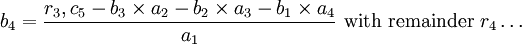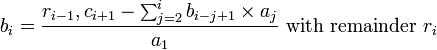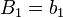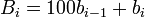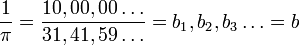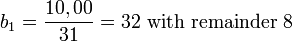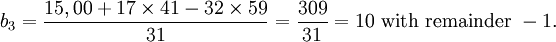Fourier division

Fourier division or cross division is a pencil-and-paper method of division which helps to simplify the process when the divisor has more than two digits. It was invented by Joseph Fourier.

Method

The following exposition assumes that the numbers are broken into two-digit pieces, separated by commas: e.g. 3456 becomes 34,56. In general x,y denotes x·100 + y and x,y,z denotes x·10000 + y·100 + z, etc.

Suppose that we wish to divide c by a, to obtain the result b. (So a × b = c.)

\frac{c}{a}=\frac{c_1,c_2,c_3,c_4,c_5\dots}{a_1,a_2,a_3,a_4,a_5\dots}=b_1,b_2,b_3,b_4,b_5\dots = b

Note that a₁ may not have a leading zero; it should stand alone as a two-digit number.

We can find the successive terms b₁, b₂, etc., using the following formulae:

b_1=\frac{c_1,c_2}{a_1}\mbox{ with remainder }r_1

b_2=\frac{r_1,c_3 - b_1\times a_2}{a_1}\mbox{ with remainder }r_2

b_3=\frac{r_2,c_4 - b_2\times a_2 - b_1\times a_3}{a_1}\mbox{ with remainder }r_3

b_4=\frac{r_3,c_5 - b_3\times a_2 - b_2\times a_3 - b_1\times a_4}{a_1}\mbox{ with remainder }r_4 \dots

Each time we add a term to the numerator until it has as many terms as a. From then on, the number of terms remains constant, so there is no increase in difficulty. Once we have as much precision as we need, we use an estimate to place the decimal point.

It will often be the case that one of the b terms will be negative. For example, 93,−12 denotes 9288, while −16,32 denotes −1600 + 32 or −1568. (Note: 45,−16,32 denotes 448432.) Care must be taken with the signs of the remainders also.

The general term is

b_i=\frac{r_{i-1},c_{i+1} - \textstyle \sum_{j=2}^i b_{i-j+1}\times a_j}{a_1}\mbox{ with remainder }r_i

Partial quotients with more than two digits

In cases where one or more of the b terms has more than two digits, the final quotient value b cannot be constructed simply by concatenating the digit pairs. Instead, each term, starting with 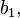$b_1,$ should be multiplied by 100, and the next term added (or, if negative, subtracted). This result should be multiplied by 100, and the next term added or subtracted, etc., until all terms are exhausted. In other words, we construct partial sums of the b terms:

B_1 = b_1

B_i = 100b_{i-1} + b_i

The last partial sum is the value for b.

Example

Find the reciprocal of π ≈ 3.14159.

\frac{1}{\pi}=\frac{10,00,00\dots}{31,41,59\dots}=b_1,b_2,b_3\dots = b

b_1=\frac{10,00}{31}=32\mbox{ with remainder }8

b_2=\frac{8,00 - 32\times 41}{31}=\frac{-512}{31}=-17\mbox{ with remainder }15

b_3=\frac{15,00 + 17\times 41 - 32\times 59}{31}=\frac{309}{31}=10\mbox{ with remainder }-1.

The result is 32,-17,10 or 31,83,10 yielding 0.318310.

Bibliography

Ronald W Doerfler. Dead Reckoning: Calculating without Instruments. Gulf Publishing, 1993.

External links

Alternative Division Algorithms: Double Division

This article is issued from Wikipedia - version of the 11/11/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.