Firoozbakht's conjecture

Prime gap function

In number theory, Firoozbakht’s conjecture (or the Firoozbakht conjecture^[1]^[2]) is a conjecture about the distribution of prime numbers. It is named after the Iranian mathematician Farideh Firoozbakht from the University of Isfahan who stated it first in 1982.

The conjecture states that $p_{n}^{1/n}$ (where $p_{n}$ is the nth prime) is a strictly decreasing function of n, i.e.,

p_{{n+1}}^{{1/(n+1)}}<p_{n}^{{1/n}}{\text{ for all }}n\geq 1.

Equivalently: $p_{{n+1}}<p_{n}^{{1+{\frac {1}{n}}}}{\text{ for all }}n\geq 1,$ see A182134, A246782.

By using a table of maximal gaps, Farideh Firoozbakht verified her conjecture up to 4.444×10¹².^[2] Now with more extensive tables of maximal gaps, the conjecture has been verified for all primes below 4×10¹⁸.^[3]

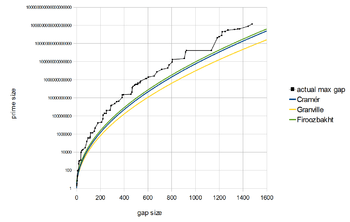
If the conjecture were true, then the prime gap function $g_{n}=p_{{n+1}}-p_{n}$ would satisfy $g_{n}<(\log p_{n})^{2}-\log p_{n}{\text{ for all }}n>4$ ^[4] and, moreover, $g_{n}<(\log p_{n})^{2}-\log p_{n}-1{\text{ for all }}n>9$ ;^[5] see also A111943. This is among the strongest upper bounds conjectured for prime gaps, even somewhat stronger than the Cramér and Shanks conjectures.^[6] It implies a strong form of Cramér's conjecture and is hence is inconsistent with the heuristics of Granville and Pintz^[7]^[8]^[9] and of Maier^[10]^[11] which suggest that $g_{n}>{\frac {2-\varepsilon }{e^{\gamma }}}(\log p_{n})^{2}$ infinitely often for any $\varepsilon>0,$ where $\gamma$ denotes the Euler–Mascheroni constant.

Two related conjectures (see the comments of A182514) are

\left(\frac{\log(p_{n+1})}{\log(p_n)}\right)^n < e

which is weaker, and

\left(\frac{p_{n+1}}{p_n}\right)^n < n\log(n)

for all values with

n > 5

which is stronger.

Notes

↑ Ribenboim, Paulo. The Little Book of Bigger Primes Second Edition. Springer-Verlag. p. 185.
1 2 Rivera, Carlos. "Conjecture 30. The Firoozbakht Conjecture". Retrieved 22 August 2012.
↑ Gaps between consecutive primes
↑ Sinha, Nilotpal Kanti (2010), On a new property of primes that leads to a generalization of Cramer's conjecture, pp. 1–10, arXiv:1010.1399 .
↑ Kourbatov, Alexei (2015), "Upper bounds for prime gaps related to Firoozbakht's conjecture", Journal of Integer Sequences, 18 (Article 15.11.2), arXiv:1506.03042 .
↑ Kourbatov, Alexei. "prime Gaps: Firoozbakht Conjecture".
↑ Granville, A. (1995), "Harald Cramér and the distribution of prime numbers" (PDF), Scandinavian Actuarial Journal, 1: 12–28 .
↑ Granville, Andrew (1995), "Unexpected irregularities in the distribution of prime numbers" (PDF), Proceedings of the International Congress of Mathematicians, 1: 388–399 .
↑ Pintz, János (2007), "Cramér vs. Cramér: On Cramér's probabilistic model for primes", Funct. Approx. Comment. Math., 37 (2): 232–471
↑ Leonard Adleman and Kevin McCurley, Open Problems in Number Theoretic Complexity, II. Algorithmic number theory (Ithaca, NY, 1994), 291–322, Lecture Notes in Comput. Sci., 877, Springer, Berlin, 1994.
↑ Maier, Helmut (1985), "Primes in short intervals", The Michigan Mathematical Journal, 32 (2): 221–225, doi:10.1307/mmj/1029003189, ISSN 0026-2285, MR 783576, Zbl 0569.10023

References

Ribenboim, Paulo (2004). The Little Book of Bigger Primes Second Edition. Springer-Verlag. ISBN 0-387-20169-6.
Riesel, Hans (1985). Prime Numbers and Computer Methods for Factorization, Second Edition. Birkhauser. ISBN 3-7643-3291-3.

Prime number classes

By formula	Fermat (2^2ⁿ + 1) Mersenne (2^p − 1) Double Mersenne (2^{2^p−1} − 1) Wagstaff (2^p + 1)/3 Proth (k·2ⁿ + 1) Factorial (n! ± 1) Primorial (p_n# ± 1) Euclid (p_n# + 1) Pythagorean (4n + 1) Pierpont (2^u·3^v + 1) Quartan (x⁴ + y⁴) Solinas (2^a ± 2^b ± 1) Cullen (n·2ⁿ + 1) Woodall (n·2ⁿ − 1) Cuban (x³ − y³)/(x − y) Carol (2ⁿ − 1)² − 2 Kynea (2ⁿ + 1)² − 2 Leyland (x^y + y^x) Thabit (3·2ⁿ − 1) Mills (floor(A^3ⁿ))

By integer sequence	Fibonacci Lucas Pell Newman–Shanks–Williams Perrin Partitions Bell Motzkin

By property	Wieferich (pair) Wall–Sun–Sun Wolstenholme Wilson Lucky Fortunate Ramanujan Pillai Regular Strong Stern Supersingular (elliptic curve) Supersingular (moonshine theory) Good Super Higgs Highly cototient

Base-dependent	Happy Dihedral Palindromic Emirp Repunit (10ⁿ − 1)/9 Permutable Circular Truncatable Strobogrammatic Minimal Weakly Full reptend Unique Primeval Self Smarandache–Wellin

Patterns	Twin (p, p + 2) Bi-twin chain (n − 1, n + 1, 2n − 1, 2n + 1, …) Triplet (p, p + 2 or p + 4, p + 6) Quadruplet (p, p + 2, p + 6, p + 8) k−Tuple Cousin (p, p + 4) Sexy (p, p + 6) Chen Sophie Germain (p, 2p + 1) Cunningham chain (p, 2p ± 1, …) Safe (p, (p − 1)/2) Arithmetic progression (p + a·n, n = 0, 1, …) Balanced (consecutive p − n, p, p + n)

By size	Titanic (1,000+ digits) Gigantic (10,000+) Mega (1,000,000+) Largest known

Complex numbers	Eisenstein prime Gaussian prime

Composite numbers	Pseudoprime Almost prime Semiprime Interprime

Related topics	Probable prime Industrial-grade prime Illegal prime Formula for primes Prime gap

First 50 primes	2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229

List of prime numbers

Prime number conjectures

Hardy–Littlewood 1st 2nd Agoh–Giuga Andrica's Artin's Bateman–Horn Brocard's Bunyakovsky Chinese hypothesis Cramér's Dickson's Elliott–Halberstam Firoozbakht's Gilbreath's Grimm's Landau's problems Goldbach's weak Legendre's Twin prime Legendre's constant Lemoine's Mersenne Oppermann's Polignac's Pólya Redmond–Sun Schinzel's hypothesis H Waring's prime number

This article is issued from Wikipedia - version of the 11/15/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Firoozbakht's conjecture

See also

Notes

References