Final stellation of the icosahedron

Final stellation of the icosahedron
Two symmetric orthographic projections
Symmetry group	icosahedral (Ih)
Type	Stellated icosahedron, 8th of 59
Symbols	Du Val H Wenninger: W42
Elements (As a star polyhedron)	F = 20, E = 90 V = 60 (χ = −10)
Elements (As a simple polyhedron)	F = 180, E = 270, V = 92 (χ = 2)
Properties (As a star polyhedron)	Vertex-transitive, face-transitive
Stellation diagram Stellation core Convex hull Icosahedron truncated icosahedron

In geometry, the complete or final stellation of the icosahedron^[1][2] is the outermost stellation of the icosahedron, and is "complete" and "final" because it includes all of the cells in the icosahedron's stellation diagram.

This polyhedron is the seventeenth stellation of the icosahedron, and given as Wenninger model index 42.

As a geometrical figure, it has two interpretations, described below:

• As an irregular star (self-intersecting) polyhedron with 20 identical self-intersecting enneagrammic faces, 90 edges, 60 vertices.
• As a simple polyhedron with 180 triangular faces (60 isosceles, 120 scalene), 270 edges, and 92 vertices. This interpretation is useful for polyhedron model building.

Johannes Kepler researched stellations that create regular star polyhedra (the Kepler-Poinsot polyhedra) in 1619, but the complete icosahedron, with irregular faces, was first studied in 1900 by Max Brückner.

History

Brückner's model (Taf. XI, Fig. 14, 1900)[3]

The echidna

• 1619: In Harmonices Mundi, Johannes Kepler first applied the stellation process, recognizing the small stellated dodecahedron and great stellated dodecahedron as regular polyhedra.^[4]
• 1809: Louis Poinsot rediscovered Kepler's polyhedra and two more, the great icosahedron and great dodecahedron as regular star polyhedra, now called the Kepler–Poinsot polyhedra.^[5]
• 1812: Augustin-Louis Cauchy made a further enumeration of star polyhedra, proving there are only 4 regular star polyhedra.^[6]
• 1900: Max Brückner extended the stellation theory beyond regular forms, and identified ten stellations of the icosahedron, including the complete stellation.^[3]
• 1924: A.H. Wheeler in 1924 published a list of 20 stellation forms (22 including reflective copies), also including the complete stellation.^[7]
• 1938: In their 1938 book The Fifty Nine Icosahedra, H. S. M. Coxeter, P. Du Val, H. T. Flather and J. F. Petrie stated a set of stellation rules for the regular icosahedron and gave a systematic enumeration of the fifty-nine stellations which conform to those rules. The complete stellation is referenced as the eighth in the book.
• 1974: In Wenninger's 1974 book Polyhedron Models, the final stellation of the icosahedron is included as the 17th model of stellated icosahedra with index number W₄₂.
• 1995: Andrew Hume named it in his Netlib polyhedral database as the echidnahedron^[8] (the echidna, or spiny anteater is a small mammal that is covered with coarse hair and spines and which curls up in a ball to protect itself).

Interpretations

Stellation diagram of the icosahedron with numbered cells. The complete icosahedron is formed from all the cells in the stellation, but only the outermost regions, labelled "13" in the diagram, are visible.

As a stellation

The stellation of a polyhedron extends the faces of a polyhedron into infinite planes and generates a new polyhedron that is bounded by these planes as faces and the intersections of these planes as edges. The Fifty Nine Icosahedra enumerates the stellations of the regular icosahedron, according to a set of rules put forward by J. C. P. Miller, including the complete stellation. The Du Val symbol of the complete stellation is H, because it includes all cells in the stellation diagram up to and including the outermost "h" layer.^[6]

As a simple polyhedron

A polyhedral model can be constructed by 12 sets of faces, each folded into a group of five pyramids.

As a simple, visible surface polyhedron, the outward form of the final stellation is composed of 180 triangular faces, which are the outermost triangular regions in the stellation diagram. These join along 270 edges, which in turn meet at 92 vertices, with an Euler characteristic of 2.^[9]

The 92 vertices lie on the surfaces of three concentric spheres. The innermost group of 20 vertices form the vertices of a regular dodecahedron; the next layer of 12 form the vertices of a regular icosahedron; and the outer layer of 60 form the vertices of a nonuniform truncated icosahedron. The radii of these spheres are in the ratio^[10]

Convex hulls of each sphere of vertices

Inner	Middle	Outer	All three
20 vertices	12 vertices	60 vertices	92 vertices
Dodecahedron	Icosahedron	Nonuniform truncated icosahedron	Complete icosahedron

When regarded as a three-dimensional solid object with edge lengths a, φa, φ²a and φ²a√2 (where φ is the golden ratio) the complete icosahedron has surface area^[10]

and volume^[10]

As a star polyhedron

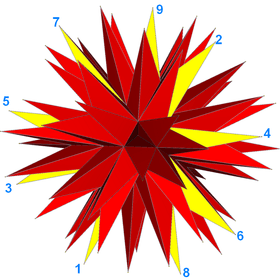Twenty (9/4) polygon faces (one face is drawn yellow with 9 vertices labeled.)

2-isogonal (9/4) faces

The complete stellation can also be seen as a self-intersecting star polyhedron having 20 faces corresponding to the 20 faces of the underlying icosahedron. Each face is an irregular 9/4 star polygon, or enneagram.^[6] Since three faces meet at each vertex it has 20 × 9 / 3 = 60 vertices (these are the outermost layer of visible vertices and form the tips of the "spines") and 20 × 9 / 2 = 90 edges (each edge of the star polyhedron includes and connects two of the 180 visible edges).

When regarded as a star icosahedron, the complete stellation is a noble polyhedron, because it is both isohedral (face-transitive) and isogonal (vertex-transitive).

See also

• Kepler–Poinsot polyhedron
• List of Wenninger polyhedron models

Notes

References

• Brückner, Max (1900). Vielecke und Vielflache: Theorie und Geschichte. Leipzig: B.G. Treubner. ISBN 978-1-4181-6590-1. (German) WorldCat English: Polygons and Polyhedra: Theory and History. Photographs of models: Tafel VIII (Plate VIII), etc. High res. scans.
• A. H. Wheeler, Certain forms of the icosahedron and a method for deriving and designating higher polyhedra, Proc. Internat. Math. Congress, Toronto, 1924, Vol. 1, pp 701–708
• H.S.M. Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, 3.6 6.2 Stellating the Platonic solids, pp. 96–104
• Coxeter, Harold Scott MacDonald; Du Val, P.; Flather, H. T.; Petrie, J. F. (1999), The fifty-nine icosahedra (3rd ed.), Tarquin, ISBN 978-1-899618-32-3, MR 676126  (1st Edn University of Toronto (1938))
• Wenninger, Magnus J., Polyhedron models; Cambridge University Press, 1st Edn (1983), Ppbk (2003). ISBN 978-0-521-09859-5. (Model 42, p 65, Final stellation of the icosahedron)
• Cromwell, Peter R. (1997). Polyhedra. Cambridge University Press. ISBN 0-521-66405-5. 
• Jenkins, Gerald, and Magdalen Bear. The Final Stellation of the Icosahedron: An Advanced Mathematical Model to Cut Out and Glue Together. Norfolk, England: Tarquin Publications, 1985. ISBN 978-0-906212-48-6.

External links

• With instructions for constructing a model of the echidnahedron (.doc) by Ralph Jones
• Towards stellating the icosahedron and faceting the dodecahedron by Guy Inchbald
• Weisstein, Eric W. "Fifty nine icosahedron stellations". MathWorld. 

• • Weisstein, Eric W. "Echidnahedron". MathWorld. 

• Stellations of the icosahedron
• 59 Stellations of the Icosahedron
• VRML model: http://www.georgehart.com/virtual-polyhedra/vrml/echidnahedron.wrl
• Netlib: Polyhedron database, model 141

Notable stellations of the icosahedron
Regular	Uniform duals			Regular compounds			Regular star	Others
(Convex) icosahedron	Small triambic icosahedron	Medial triambic icosahedron	Great triambic icosahedron	Compound of five octahedra	Compound of five tetrahedra	Compound of ten tetrahedra	Great icosahedron	Excavated dodecahedron	Final stellation
The stellation process on the icosahedron creates a number of related polyhedra and compounds with icosahedral symmetry.