Fermi coordinates
In the mathematical theory of Riemannian geometry, Fermi coordinates are local coordinates that are adapted to a geodesic.[1]
More formally, suppose M is an n-dimensional Riemannian manifold, 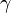 is a geodesic on
is a geodesic on 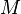 , and
, and 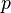 is a point on
is a point on 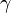 . Then there exists local coordinates
. Then there exists local coordinates 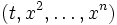 around
around 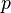 such that:
such that:
- For small t,
 represents the geodesic near
represents the geodesic near 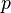 ,
, - On
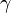 , the metric tensor is the Euclidean metric,
, the metric tensor is the Euclidean metric, - On
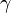 , all Christoffel symbols vanish.
, all Christoffel symbols vanish.
Such coordinates are called Fermi coordinates and are named after the Italian physicist Enrico Fermi. The above properties are only valid on the geodesic. For example, if all Christoffel symbols vanish near 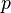 , then the manifold is flat near
, then the manifold is flat near 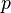 .
.
- ↑ Manasse and Misner , Fermi Normal Coordinates and Some Basic Concepts in Differential Geometry. Journal of Mathematical Physics 4:6, 1963.
See also
This article is issued from Wikipedia - version of the 5/17/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.