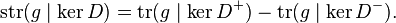Equivariant index theorem

In differential geometry, the equivariant index theorem, of which there are several variants, computes the (graded) trace of an element of a compact Lie group acting in given setting in terms of the integral over the fixed points of the element. If the element is neutral, then the theorem reduces to the usual index theorem.

The classical formula such as the Atiyah–Bott formula is a special case of the theorem.

Statement

Let \pi: E \to M be a clifford module bundle. Assume a compact Lie group G acts on both E and M so that \pi is equivariant. Let E be given a connection that is compatible with the action of G. Finally, let D be a Dirac operator on E associated to the given data. In particular, D commutes with G and thus the kernel of D is a finite-dimensional representation of G.

The equivariant index of E is a virtual character given by taking the supertrace:

\operatorname{str}(g\mid\ker D) = \operatorname{tr}(g\mid\ker D^+) - \operatorname{tr}(g\mid\ker D^-).

See also

References


This article is issued from Wikipedia - version of the 7/31/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.